 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
It's All about 64



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
It's all about $64$
I was with a class of children in Bromley near to London, when I suddenly came up with this idea, and I put it to the youngsters at the school. They did a lot of work on it so I thought I'd share it with you.
It's all about $64$!
Lots of you know that $64$ is $8$ times $8$. So if you were asked to write down all the numbers up to $64$ you might decide to do eight lots of $8$ . [It's a bit like $100$ in that you may well write ten lots of $10$ to get up to $100$ and produce a $100$ square.]
I suggested to them that they tried writing the numbers up to $64$ in an interesting way so that the shape they made at the end would be interesting, different, more exciting ... than just a square. Here are the ones that some of them came up with to show that the numbers could be arranged in an interesting way.
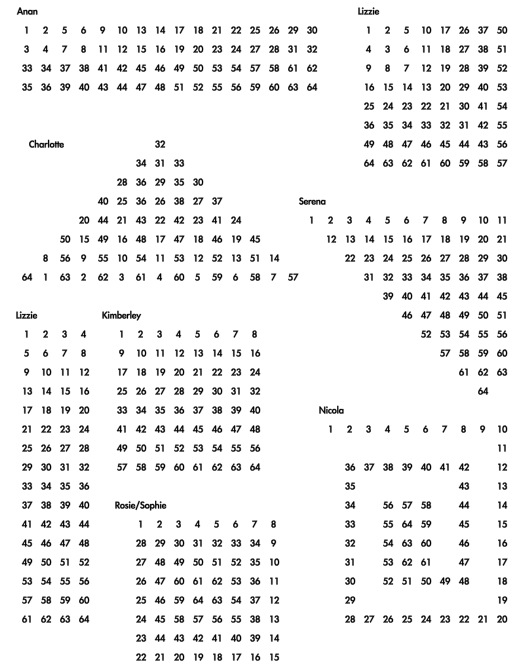
Most of them, as you see, ended up with shapes that were not squares. Those that did end up with an $8$ by $8$ square put the numbers in an interesting order into the shape.
When they did that they were then asked to made a tile [or frame] that was made up of four squares.
Here are some examples:-
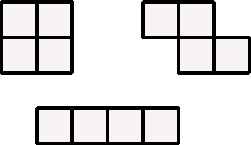
The idea now was to place one these tiles/frames somewhere on the table of $64$ so that it covered four numbers. [The tiles were made so that the squares were the same size as the squares on each of the numbers in the $64$ table.]
The numbers underneath the tile/frame were added up and recorded. The tile/frame was then moved around the table of $64$ to different positions and each time the total of the four numbers underneath was recorded.
Well that's what you need to do. It's fun creating new $64$ tables in different shapes.
Lastly of course you need to ask, "I wonder what would happen if ...?"