 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Building with Longer Rods



- Problem
- Teachers' Resources
Building with Longer Rods
This activity has been particularly created for the most able.
When you have completed Building with Rods then go further with this challenge of using rods that are $3$ units long.
Same rules as before - so just to remind you; here are two solutions that fit the rule.
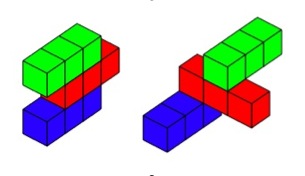
Here are two that don't fit the rule as the small cubes have to be lined up squarely, with no overlapping.
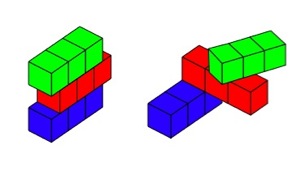
The challenge is to find all the possible ways of stacking the rods, keeping the blue rod on the bottom, the red rod in the middle and the green rod on top.
What do you think will happen if you try the same activity with rods that are $4$ long?
What do you think will happen if the rods are $5$ long?
Why do this problem?
Possible approach
Key questions
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.