 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Parabolas Again



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
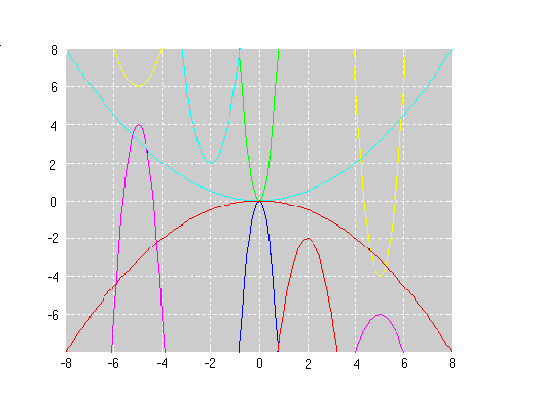
This problem was solved by Ali Abu Hijleh, age 13, Alex Liao, age 14 and Prateek Mehrotra, age 14 from Riccarton High School, Christchurch, New Zealand and Andrei Lazanu, age: 12 from School No. 205, Bucharest, Romania. Well done all of you. This is Andrei's solution:
I observed that the equations of the parabolas given in the problem are of the form: $y = a(x + b)^2 + c$
where positive corresponds to parabolas with the opening towards the top, and negative to parabolas with the opening towards the bottom; are the coordinates of the peak. I identified the parabolas in your pattern and I verified them with the help of a small program in Matlab:
x=-8:0.1:8
y1=-2*(x+6).*(x+6)-2
y2=-2*(x+4).*(x+4)-1
y3=-2*(x+2).*(x+2);
y4=-2*x.*x+1;
y5=-2*(x-2).*(x-2)+2;
y6=-2*(x-4).*(x-4)+3;
y7=-2*(x-6).*(x-6)+4;
y8=2*(x+6).*(x+6)+2;
y9=2*(x+4).*(x+4)+1;
y10=2*(x+2).*(x+2);
y11=2*x.*x-1;
y12=2*(x-2).*(x-2)-2;
y13=2*(x-4).*(x-4)-3;
y14=2*(x-6).*(x-6)-4;
plot(x,y1,x,y2,x,y3,x,y4,x,y5,x,y6,x,y7,x,y8,x,y9,x,y10,x,y11,x,y12,x,y13,x,y14)
hold
axis([-8 8 -4 4]);
grid
Consequently, the equations of the 14 parabolas in your pattern are:
$y = -2(x + 6)^2 - 2$
$y = -2(x + 4)^2 - 1$
$y = -2(x + 2)^2$
$y = -2x^2 + 1$
$y = -2(x - 2)^2 + 2$
$y = -2(x - 4)^2 + 3$
$y = -2(x - 6)^2 + 4$
$y = 2(x + 6)^2 + 2$
$y = 2(x + 4)^2 + 1$
$y = 2(x + 2)^2$
$y = 2x^2 - 1$
$y = 2(x - 2)^2 - 2$
$y = 2(x - 4)^2 - 3$
$y = 2(x - 6)^2 - 4$
Andrei supplied the Matlab program but in order to challenge you to find his equations it is not reproduced here