 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Bracelets



Well, in this country, and perhaps in yours, lots of young folk are wearing bracelets - both girls and boys. I was looking at some that my students wear and found that some were magnetic!
Many seem to have beads that are spherical and they go around the wrist quite comfortably. There are lots of different sizes and some have large beads and some quite small beads.
I suppose that most wrists are kind of oval - squashed circles - in shape and with the string or wire through the beads they fit very well.
It was playing with the magnetic beads off the person's wrist that gave me some ideas. There were $18$ beads altogether and they were all the same colour but I've chosen to show them in a variety of colours!
I found I could put them into different shapes:-
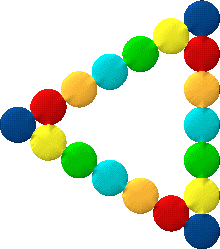
mind you, you'd have to have a triangular wrist for them to stay like that!
Now suppose we play around with this idea and make a rule that there has to be some shaped hole in the middle for a wrist. But we'll allow that to be all kinds of shapes :- vaguely triangular, rectangular, hexagonal etc.
You could try this out with marbles, circular counters, tiddly-winks, coins or with a drawing program on your computer.
I think we'll make a rule that the circles/spheres have to be the same size and you don't have to imagine that they're magnetic!
So here are some that I found with $18$ beads:-

I liked that one as it is the longest rectangle you could make - remembering to keep a wrist-hole. I then went on to:-

and then, almost a square :-

I like the next one - although it was a little hard to do on the computer!

Have a go at making these with your circles!
I then moved on to $24$ circles - it seemed to be a "good" number to choose - I wonder why?
I managed to get this regular shape:-

But then I thought that since I had $24$, perhaps I could make two that were exactly the same. So there's a new rule: You can make more than one bracelet as long as they're both the same.
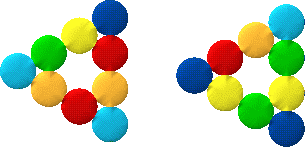
Have a go at using $24$ circles and make a large triangle and a fat square.
Well, now it's time to explore, to see what other bracelets you can make. Remember that there's to be a "wrist-hole". The shapes should be kind of "regular" but not strictly so, because then we could not use rectangles.
Other things to investigate:-
- If you make a particular shape with $18$ and then the next size
up comes when you use $24$, is there going to be the next size up
at $30$?
So whatever shape you make, how many will you need to make the next size up? How does each shape grow? Look at the first shape I made using $24$:-

What will the next size up of this look like?
- What are good numbers of beads to use? Why?
- What's the smallest number of beads that will allow you to make two identical bracelets? Why? How many will you need to make three of those?
-
If you make a bracelet with just one thickness of beads them how many will you need to make one that has a double thickness? Here's one I did by making the wrist-hole smaller and getting it to be twice as thick:

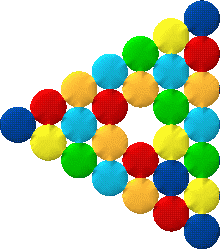
- Would cube beads lend themselves to exploring slightly differently? What about tetrahedral bead?
- What about ...?