Copyright © University of Cambridge. All rights reserved.
'Magic Letters' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem gives students opportunities to perceive structure in a simple case and make generalisations based on that structure.
While offering students a chance to practise addition in an engaging context, there will also be opportunities to appreciate the effect of combining odd and even numbers.
Possible approach
This printable worksheet may be useful: Magic Letters
Here is a video of the NRICH team presenting the challenge.
Draw 5 circles on the board in a V shape, and give students mini-whiteboards or paper.
"I want you to arrange the numbers from 1 to 5 in a V shape like mine; you can put the numbers in any order you like."
Ask students to hold up their V shapes. Divide the board into two columns, headed 'Magic' and 'Not Magic'. Select some of the class's Vs and copy them on the board in the appropriate column, according to the definition in the problem.
"While I'm writing up your Vs, be thinking about what criteria I might be using to determine whether a V is magic or not."
Once students have worked out what makes a V magic, clarify what makes Vs different; for example, these Vs are equivalent:
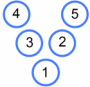
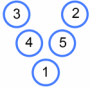
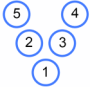
"Have we found all possible non-equivalent Magic Vs that can be made with the numbers from 1 to 5? Work with your partner to find any more, or convince yourselves that there are no more to find."
Take some time to discuss their arguments for why there are only three possible Magic Vs. Possible suggestions might touch upon:
- As the numbers from 1 to 5 add up to an odd total, the repeated number at the bottom must be odd.
- If we put a 2 or a 4 at the bottom, we'd have an odd total left over to split between the two arms, so it can't be done equally.
- If there was an even number at the bottom, there'd be three odds and one even left, so they can't be split to make the same total on each side.
"Close your eyes and imagine you wanted to make a Magic V using the numbers from 2 to 6 instead. Can you picture what the Vs could look like, using the insights you have from making the Vs with 1 to 5?"
"Now open your eyes and talk to your partner. Write down your Vs and convince each other that you found them all."
Bring the class together and share their convincing explanations.
"In a few minutes, I'm going to give you five consecutive numbers bigger than 100. I want you to be able to tell me straight away how to make the complete set of Magic Vs that use those five numbers. Talk to your partner and agree a strategy."
Once students have had a chance to consider how they will tackle the challenge, bring the class together and challenge some pairs of students to produce Magic Vs from randomly selected sets of 5 consecutive numbers.
Next, move on to exploring the arm totals of Magic Vs.
"Here is the set of Magic Vs we made with the numbers 1 to 5. The arm totals were 8, 9 and 10. In a while, I'm going to ask you to produce a Magic V with a particular arm total. You need to devise a strategy for working this out quickly."
As students are working on this, circulate and look out for students who are struggling to get started. You could prompt them:
"What were the arm totals when we used the numbers 2 to 6?"
"Why is the arm total for the V with a 2 at the bottom 3 more than the arm total for the V with a 1 at the bottom?"
"What is special about the arm total when the number at the bottom of the V is the middle number of the five consecutive numbers?"
Notice too any students who are developing efficient strategies.
If appropriate, bring the class together so that those who have developed a strategy can demonstrate (without explanation!).
Finally, bring the class together and challenge pairs to find Magic Vs with particular arm totals, sharing and explaining how they do it.
Possible support
Giving students digit cards or inviting them to write the numbers on small pieces of paper that can be moved around easily might help them to experiment with different arrangements.
Possible extension
Magic Ls, Ns and Ws can be explored in the same way.