 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Magic Letters



Magic Letters printable worksheet
The problem is explained below, but you may wish to go to the Getting Started page to watch a video of the NRICH team presenting the initial challenge.
Charlie has made a Magic V with five consecutive numbers:
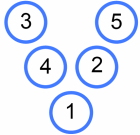
It is a Magic V because each 'arm' has the same total.
Alison drew this magic V:
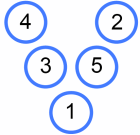
Charlie said "That's really just the same Magic V as mine!"
What do you think Charlie meant?
There are six more Magic Vs that are the same as Charlie's - can you find them all?
Click below to check you have.
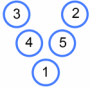
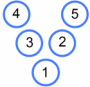
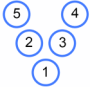
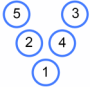
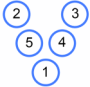
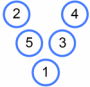
Can you find all the possible Magic Vs that use the numbers $1$ to $5$ and are different from Charlie's?
How can you be sure you have found them all?
What happens if you use the numbers from $2$ to $6$? Or from $3$ to $7$? Or $4$ to $8\dots$?
Here is a spreadsheet to help you investigate Magic Vs made from five consecutive numbers.
Can you describe an efficient strategy to find all Magic Vs for any given set of numbers?
Can you use your strategy to find all the possible Magic Vs that use the numbers $987, 988, 989, 990, 991$?
Can you find a Magic V where each arm has a total of 60? Or 1000? Or...?
Can you find more than one?
Can you find a Magic V for any arm total?
Charlie and Alison drew some more letters, to see if they could make them magic - that is, using consecutive numbers to make equal arm totals.
| Magic L? | Magic N? | Magic W? |
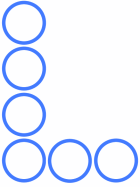 |
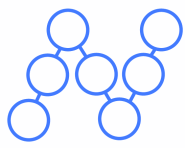 |
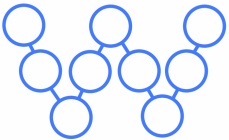 |
Investigate some of these Magic Letters in the same way that you explored Magic Vs.
What general conclusions can you reach?
You can use this spreadsheet to explore.
Click here for a poster version of Magic Vs.