 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
The Big Cheese



I met up with some friends yesterday for lunch. On the table was a good big block of cheese. It looked rather like a cube. As the meal went on we started cutting off slices, but these got smaller and smaller! It got me thinking ...
What if the cheese cube was $5$ by $5$ by $5$ and each slice was always $1$ thick?
It wouldn't be fair on everyone else's lunch if I cut up the real cheese so I made a model out of multilink cubes:
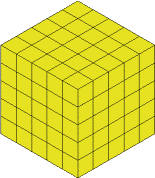
You could of course, just make $5$ slices but I wanted to have a go at something else - keeping what is left as close to being a cube as possible.
You can see that it's a $5$ by $5$ by $5$ because of the individual cubes, so the slices will have to be $1$ cube thick.
So let's take a slice off the right hand side, I've coloured it in so you can see which bit I'm talking about:
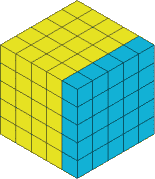 This now gets cut off and we have:
This now gets cut off and we have: 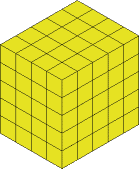
The next slice will be from the left hand side (shown in a different colour again):
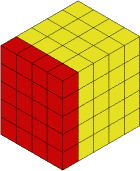 Well the knife cuts and we are left with:
Well the knife cuts and we are left with: 
Remember I'm setting myself the task of cutting so that I am left with a shape as close to a cube shape as possible each time.
So the next cut is from the top. Hard to cut this so I would have put it on its side!
 I'll remove that and I'm left with the $4$ by $4$ by $4$ cube
I'll remove that and I'm left with the $4$ by $4$ by $4$ cube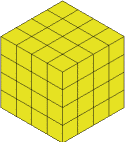
I do three more cuts to get to the $3$ by $3$ by $3$ and these leave the block like this:





 and then onto:
and then onto: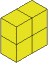


That leaves you with two of the smallest size cube $1$ by $1$ by $1$.
If we keep all the slices and the last little cube, we will have pieces that look like (seen from above):
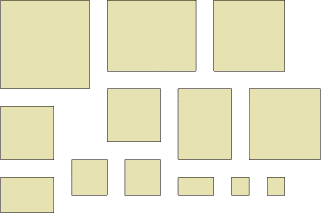
C H A L L E N G E
Now we have thirteen objects to explore.- What about the areas of these as seen from above?
- What about the total surface areas of these?
- What about their volumes of the pieces?
A L S O
Investigate sharing these thirteen pieces out so that everyone gets an equal share.
What about ...?
I guess that once you've explored the pattern of numbers you'll be able to extend it as if you had started with a $10$ by $10$ by $10$ cube of cheese.
