 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
More Parabolic Patterns



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We have received solutions from Sarah (Madras College, St Andrews), Andrei (School no. 205, Bucharest, Romania) and from Ryan and Belinda (Riccarton High School, Christchurch, New Zealand). Well done to you all.
All approached the problem in a similar way. Ryan and Belinda's response follows:
To get the lines curving downward from the top
We are given the equation for the middle curve (that goes through the point $(0,0)$) which is $y=x^2$. From there we add or subtract $2$ to give the curves going through the points $(0,2)$ and $(0,-2)$ respectively, giving the equations -
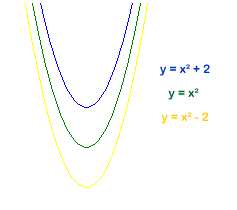
To get the lines curving upward from the bottom
This is a reflection of the downward curves, so we use opposite equations, e.g. instead of $y=x^2$we use $y=-x^2$. From there we add or subtract $2$ to give the curves going through the points $(0,2)$ and $(0,-2)$ respectively, giving the equations -
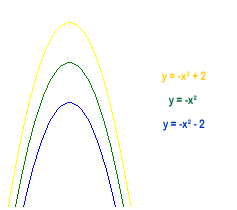
To get the lines curving from right to left
We are given the equation for the middle curve (that goes through the point $(0,0)$) which is $x=y^2$. From there we add or subtract $2$ to give the curves going through the points $(2,0)$ and $(-2,0)$ respectively, giving the equations -
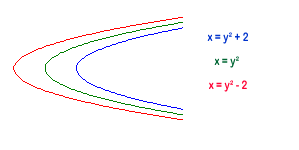
To get the lines curving from left to right
This is a reflection of the right to left curves, so we use opposite equations, e.g. instead of $x=y^2$we use $x=-y^2$. From there we add or subtract $2$ to give the curves going through the points $(2,0)$ and $(-2,0)$ respectively, giving the equations -
