Why do this problem?

Many students are accustomed to using number patterns in order to generalise. This problem offers an alternative approach, challenging students to consider multiple ways of looking at the structure of the problem and making sense of other people's approaches, an important part of working mathematically.

The powerful insights from these multiple approaches can help us to derive general formulae, and can lead to students' appreciation of the equivalence of different algebraic expressions.

Possible approach

These printable resources may be useful:
Steel Cables
Steel Cables Intro
Steel Cables Templates
Steel Cables - Methods

Start by showing this image:

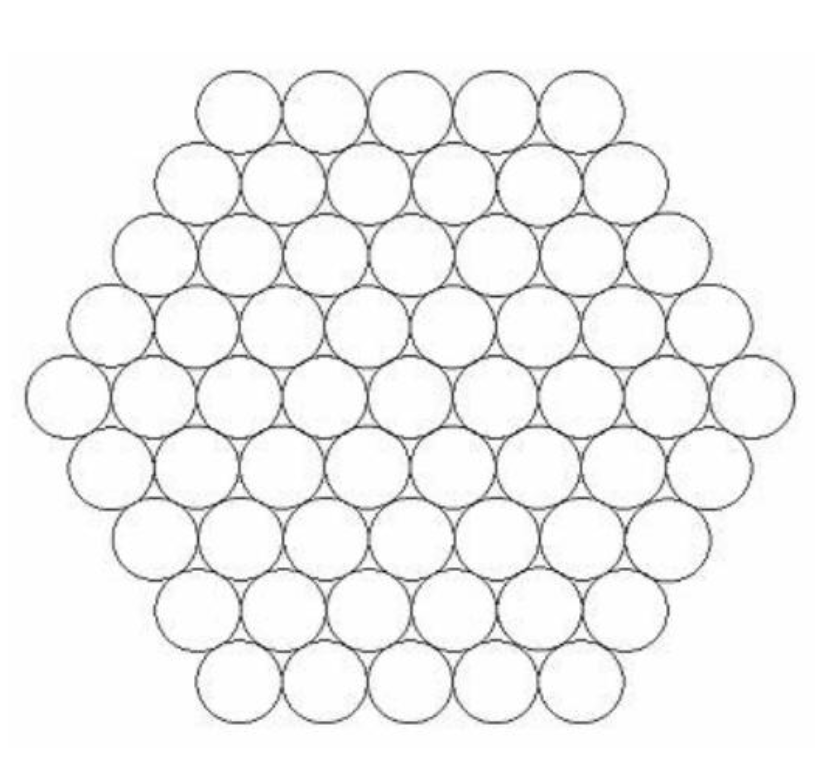
"Cables can be made stronger by compacting them together in a hexagonal formation. Here is a 'size 5' cable. Can you work out, without counting every strand, how many strands it contains?"

Give students a short time to consider this and then discuss their ideas in pairs, before bringing the class back together to share their different methods.

Hand out this worksheet, together with these templates, and ask:

"How many strands are needed for a size 10 cable?"
"While you are working on this, keep in mind how your method could be adapted to work out the number of strands needed for any size of cable."

While students are working, circulate and observe any interesting methods that students are using. When the class is ready, bring them back together and invite those students with an interesting method to explain what they did.

"Here is some work done by a group of students in another school, who were asked to find a formula to work out the strands needed for a size n cable."

Arrange the class in groups of four, and hand out one of the four pictures from this worksheet to each student.

"I'd like each of you to make sense of the picture I have given you, and work out how to use it to solve the problem. Then, when you are ready, explain your method to the rest of your group. Finally, your group needs to agree on which of the four approaches makes the most sense to you, and be prepared to justify your choice to the rest of the class."

To finish off, each group can explain to the rest of the class which approach they chose, and why.

Key questions

Is there a quick way of adding up all the numbers from 1 to n?
Look at the picture for a size 5 cable. What might the group have drawn for a size 6 cable?

Possible support

Seven Squares gives lots of simple contexts where formulae emerge by looking at structure rather than number sequences.

Picturing Triangle Numbers, Mystic Rose, and Handshakes introduce students to summing consecutive numbers, which is a feature of several of the solutions used by the groups in the problem.

Possible extension

Challenge students to come up with alternative, elegant ways of computing the number of strands in a size n cable.

The problems Summing Squares and Picture Story lead to formulae for some intriguing sequences through analysis of structure.

To read one teacher's account of using this problem, click here.