Copyright © University of Cambridge. All rights reserved.
'Steel Cables' printed from https://nrich.maths.org/
Show menu
Do you know a quick way of adding up all the numbers from 1 to n?
If not, take a look at the problem Picturing Triangle Numbers.
Below are student diagrams from the problem page, but they now also show the working that the students used to explain their diagrams. Can you explain their reasoning?
Group 1
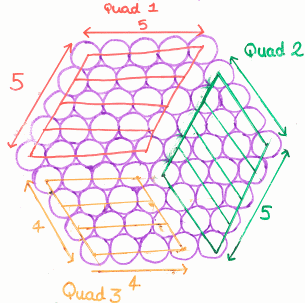
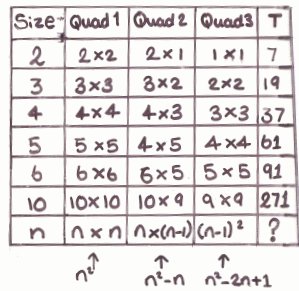
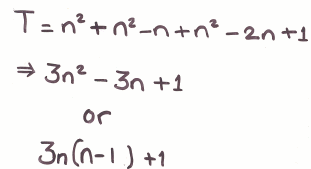
Group 2

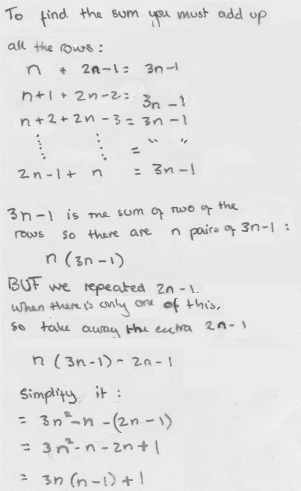
Group 3
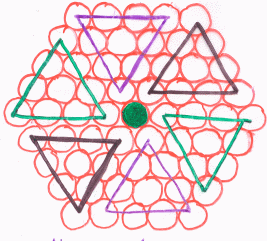
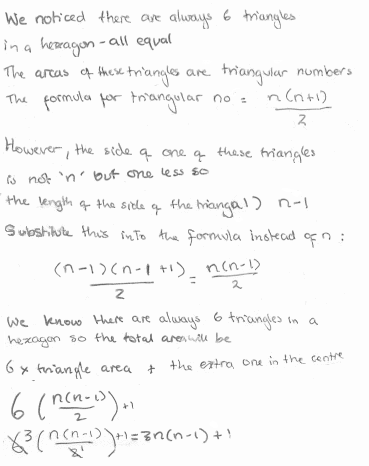
Group 4
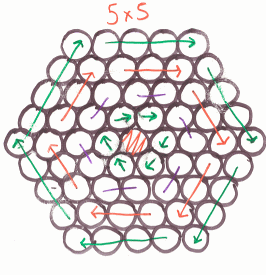

If you are finding it difficult to make sense of the different groups' work, try to work out what they might have drawn for a size 6 cable.