 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Which Scripts?



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to everybody who worked out which numbers belong to which scripts!
Poppy from Acomb First School in the UK shared this strategy with us:
First of all I found the numbers that I recognised. Then I found the numbers that looked a little bit like the numbers that I recognised and looked for one-digit numbers and three-digit numbers because I knew that one-digit numbers would be 2 and that three-digit numbers would be 100. Then I grouped the numbers into 5 groups of similar scripts.
To work out the trickier numbers, I was able to work out the 1 from the 100 and the 2 from the 2. Then I could work out the 13 and the 25. Once I knew the 13 and 25, I could find the 58 from the 5 and then the 83 from the 3 and the 8.
Good ideas, Poppy - lots of children found it easiest to start by looking for the digit 2. James from Co-op Academy New Islington, Manchester in the UK started by sorting the numbers into the scripts based on which numbers looked similar:
I cut the number grid into squares so I could move them around.
I found out what the six numbers in English were first because I know what they look like.
Then, I started to look for ones that looked similar. I put them in rows and columns for the the same number and the same scripts to be organised. Next, I looked for numbers in other scripts that looked very similar and and matched them up with the correct number. Because I knew 2 it was easier to work the rest of them out because after you've found 2 you can work out 25. Once you've worked out 25 you can work out 58. Once you've worked out 58 you can work out 83. After you've worked out 83 you can work out 13. For the 100s you can use the 1 from 13 and there are three digits or two zeroes or two dots on some of them.
This is a good step-by-step method, James! The numbers we use in English are also the same numbers that are used in many other languages. I wonder if anyone knows the name for these numbers?
We received a lot of solutions from the children at St. Helen's School in Abbotsham, England. Amelia-May and Frances explained their strategy, which was similar to James's:
First we looked for all the 2s (which were kind of easy), then found the 25s because we knew what the 2 would look like. After that we got the 58s because we knew what the 5 looked like. Then we found that it had an 8 like the 83 so we moved on to that looking for the 83s. We realised that the 83 linked to 13 because of the 3. So we found all of the 13s. Last but not least we did the 100!

Thank you as well to Edgar, Will, Amber, Grace, Kacie, Fraser, Oliver, Myles, Albie, Charlie and Lucy from St. Helen's School who also sent in some similar solutions.
Gabe and Muhammad from Wembrook Primary also used similar reasoning, and explained their thinking very clearly:


Dhruv from The Glasgow Academy in the UK used their prior knowledge of two of the scripts to solve this problem:
First, I separated these numbers into different groups based on their writing pattern.
Secondly, I knew numbers that were in English and Hindi because I am from India.
Thirdly, I arranged the numbers in ascending order.
Finally, for the first row in Chinese I took a guess for the first number and then linked it to find the other numbers.
Example: For the Chinese group I took a guess that the two lines were the number 2 and then found the same two lines in another number and so on.
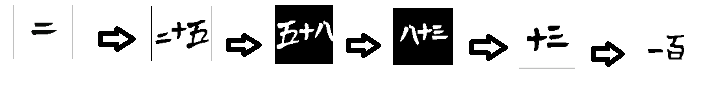
Then I arranged the numbers in ascending order.

I followed the same strategy for the two scripts which were unknown to me.
Well explained, Dhruv - this looks similar to some of the other strategies above, but the pictures make it really clear how you got from one solution to the next. I wonder if anybody has worked out what the other scripts might be?
Thank you as well to the following children for sending in their ideas about which numbers belonged to which scripts: Zoe from Canada; Chloe, Meriam, Sophia, Milan, Josh, Thomas, Hogan, Henry and Harry from Banstead Prep; Blossom, Gabe, Kinel and Lilah from Onchan Primary School on the Isle of Man; Freddie; and the children at Ganit Kreeda in Vicharvatika, India.
The second part of this problem involved writing the number 51 in each script. Only the next four groups of children sent in a correct solution to this, as lots of children made a mistake with writing 51 in the Chinese script.
Isobelle, Edie and James from Richmond Methodist School in the UK explained:
We took the 5 and the 1 from each script to make 51 in the different scripts.
I wonder if you had actually had to use a slightly different strategy with the Chinese script? Sophie from Glenfall in the UK explained:
The trickiest was the Chinese style numbers because they actually used a 'plus' symbol which wasn't a digit.
Elliott from Richmond Methodist School in the UK had an idea about what the plus symbol might mean:
The second step is to write 51 in all of the scripts. You just need to take the 5 and 1 from all the scripts except script E (the Chinese script). I saw that a + equals x10. If one of the symbols has lines going up, one line is 1, two are 2 and 3 are 3. So adding a plus after a symbol multiplies the previous symbol by 10.
Good ideas! I wonder how this works with the number 13 as there isn't a digit before the plus symbol?
Junior Maths Club at Caulfield Grammar School in Wheelers Hill, Australia sent in these full solutions:

Thank you all for sharing your ideas with us.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Roll These Dice
Roll two red dice and a green dice. Add the two numbers on the red dice and take away the number on the green. What are all the different possible answers?