Copyright © University of Cambridge. All rights reserved.
'Parabolic Patterns' printed from https://nrich.maths.org/
Show menu
Parabolic Patterns printable sheet
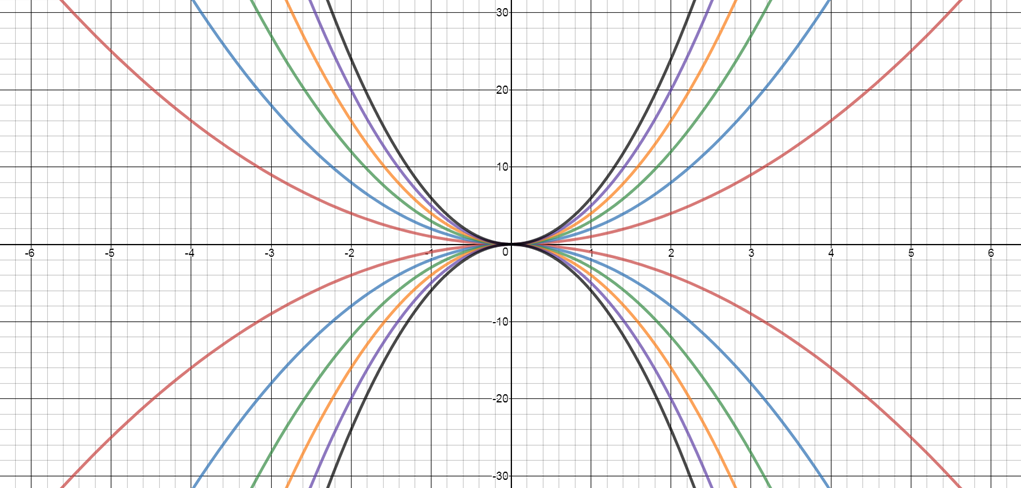
The illustration shows the graphs of fifteen functions. Two of them have equations
$y = x^2$
$y = - (x - 4)^2$

Can you find the equations of the other parabolas in the picture?
You may wish to use a graphical calculator or software such as Desmos to recreate the pattern for yourself.
Can you find the equations of these parabolas?
NOTES AND BACKGROUND
This sort of challenge is sometimes called an inverse problem because the question is posed the opposite way round to what might have been expected. This is almost like saying: 'here is the answer, what was the question?' Instead of giving the equations of some functions and asking you to sketch the graphs, this challenge gives the graphs and asks you to find their equations.
You are being asked to sketch a family of graphs. What makes this a family? All the graphs are obtained by transformations such as reflections and translations of other graphs in the family. The key is to find the simplest function and then to find transformations of the graph of that function which give the other graphs in the family.
If you have access to a graphic calculator, or to graph drawing software, it will not give you the answers. You will have to think for yourself what the equations should be and then the software will enable you to test your own theories and see if you were right.