This article first appeared in the January 2011 edition of MTi, a multi-media journal published by The Association of Teachers of Mathematics.

 

In March 2010, the NRICH website had a slightly different feel, inspired by the way teachers at Kingsfield School in Bristol work with their students. Following an introduction to a potentially rich starting point, a considerable proportion of the lesson time at Kingsfield is dedicated to working on questions and ideas generated by children. So, rather than publishing a range of problems on NRICH that month, we offered starting points for 'projects'.

 

The aim was that these projects would give learners opportunities to work together, discuss ideas, develop conjectures of their own and suggest new lines of enquiry. This is how it is to be a mathematician, working alongside other mathematicians. Children could experience this within their own classrooms, but also in the wider world through the NRICH Projects Site, an online community we set up for this purpose. By placing ideas and thoughts onto the Projects Site, after some exploration, others could share in the excitement and investigate too. It was possible to see where others had gone from the same starting point and it meant that a user could choose to explore other people's ideas further. During the months of March and April, we added problems to the main NRICH website which were based on the questions and conjectures posted by learners.

 

It was the initial discussions with Alf Coles and Tracy Wylie, both teachers at Kingsfield at the time, which prompted the format of the March NRICH site. Alf, and Tracy, led us - the NRICH team - in some mathematics in the same way they would with their learners in school. Reflecting on what we had done together, we discussed our aim to enable children to experience what it means to work like a mathematician. Part of working in this way involves asking your own questions and pursuing them, rather than always investigating a question or conjecture suggested by someone else. Alf and Tracy's approach embraced this completely and I was struck in particular by Alf's assertion that we, as teachers, should perhaps trust pupils more. By this, I mean that we should trust them to 'play with' a mathematical starting point and be able to ask their own, appropriate, questions. This led me to wonder, do I do this when I work with children? Do I really trust them? Do I really 'let go' of the mathematics and allow children the freedom to pursue their own line of enquiry?

 

I was reminded of these discussions and contemplations one Saturday as I worked with a group of Year 5 and 6 children in Warwick. This was the first time I had met the majority of the children and we began by playing the Factors and Multiples Game.

 

To start with, I used a $1$ to $50$ grid on the interactive whiteboard. The group played in two teams against each other, taking it in turns to choose a number on the grid which was either a factor, or a multiple of, the previous number. The aim of the game is to prevent your opponent from being able to select a number. You may like to think about how you would win before reading on!

 

Quite often when I play this with a group of learners, the first game can go on for a while so I might suggest that we could be here 'for ever', and therefore I encourage children to play on their own grid against a partner instead. On this Saturday, I explained that I was looking for someone to develop a strategy so that they knew they would ALWAYS win the game. We gathered together as a whole group after a short time to discuss what they thought was important so far and this brought up the significance of prime numbers. After a little more playing time, there were many pairs of children who believed they could play against me, and beat me. Having proved this was the case, I encouraged them to articulate their strategy in as general a way as possible.

 

Here is an example of the beginning of a strategy involving prime numbers (circled in red). In this case though, the player does not always win:

 

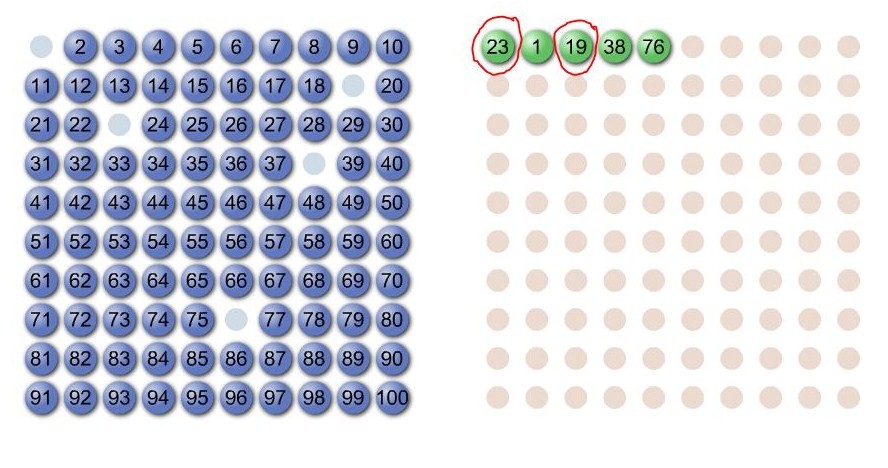
The above idea led to a winning strategy, where both prime numbers chosen are large enough that the player must win:

 

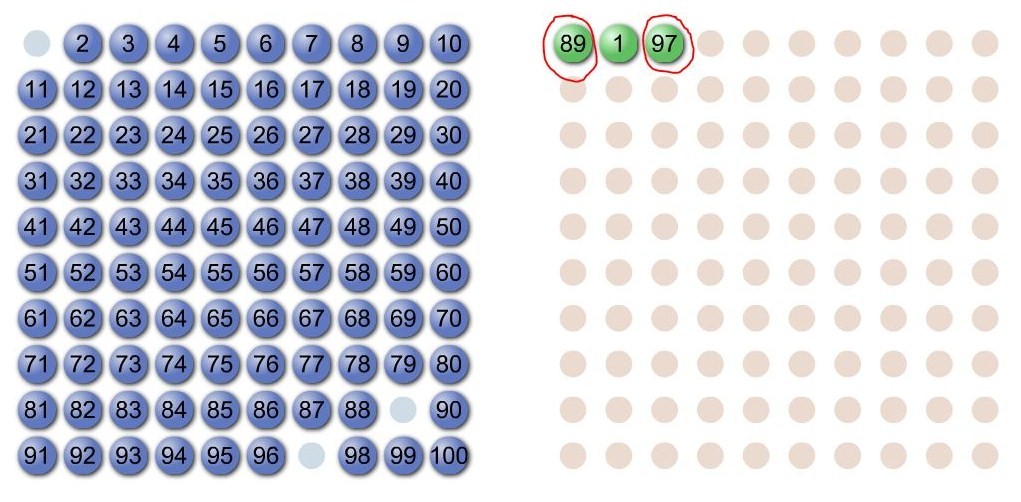
Choosing the correct primes is the crux of the winning the game, and clearly depends on the size of the grid.

 

Indeed, one of the lovely things about this game is of course its potential for 'what if...' investigations. I have to admit that I stayed in control of these 'what ifs' myself and focused on the grid size: what if we played on a $1-100$ grid? What if we played on a $1-500$ grid etc. etc ...? This in itself led to some fantastic opportunities for generalising: Imagine that your friend is about to play this game against someone else, but you don't know what the grid is going to look like. How would you advise your friend to play, so that he or she is guaranteed to win the game?

 

What emerged was a very well-articulated strategy that worked for any size grid. Or so I thought ...

 

It was at this point that one child in the group raised his hand, "What if we had a $1$ to $10$ grid?" This is one of those moments in the classroom when an on-the-spot decision can make a huge difference to the direction of the lesson. I could have said, and in some ways I'm surprised I didn't, something along the lines of, "Well, yes, we'd use the same strategy, wouldn't we?" and I'd have left it there, with a question that I didn't really expect an answer to, or rather I simply expected a nod. Instead, I said something more along the lines of "Well, let's try it".

 

So, in pairs, children tried a $1-10$ grid. Try it yourself. Intriguing? We spent a good fifteen minutes exploring this simpler case, and on two occasions one pair thought they had developed a strategy, but when putting it to the test against another pair, it didn't work. I felt such a buzz. We were all, the other adults in the room - me included, were engaged in a challenge that was a genuine challenge for each and every one of us. None of us knew the answer. We didn't even know whether it would be possible to find a strategy. How exciting! We were working like mathematicians.

 

And the question that had drawn us in was posed by a child of ten, perhaps eleven, years old. I am glad that on that occasion I did trust the pupil, but I shudder when I think how close I was to dismissing his question. I hope it has given me the push I needed to 'let go' a bit more in the future. Do I trust the learners I work with and therefore give them that freedom to ask their own questions in a genuine, meaningful way? Do you?