Tricircle
Problem
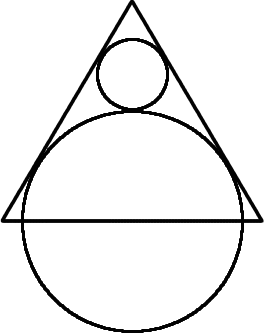
The centre of the larger circle is at the midpoint of one side of an equilateral triangle and the circle touches the other two sides of the triangle.
A smaller circle touches the larger circle and two sides of the triangle.
If the small circle has radius 1 unit, find the radius of the larger circle.
Student Solutions
This solution comes from Soh Yong Sheng (Raffles Institution, Singapore).
First he added a few lines and letters to the diagram:
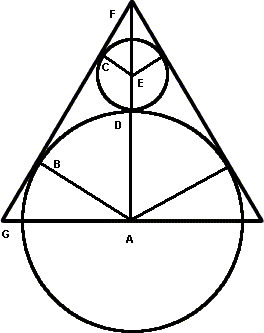
Since the circles are tangent to the triangles, we know that CE is perpendicular to GF, and AB is perpendicular to GF. [A line touching a circle (tangent) is always perpendicular to the radius which meets it.] We also see by symmetry that FA is perpendicular to AG.
The line FA bisects the original equilateral triangle, so we know that FGA=60 °, and GFA=30 °. We can now see that in triangle FCE, CEF=60 °, and in triangle ABF, BAF=60 °. So all three of these triangles have angles 30 °, 60 °, 90 °.
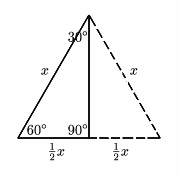
We know that CE is 1 unit, so EF = 2 units. ED is also a radius
of the small circle, so the total length of DF is 3 units.
Now in triangle ABF, FA is twice BA, but BA and DA are both radii,
and so must be the same. This means that DF is half of FA, so FA is
6 units, and DA is 3 units. This is the radius of the larger
circle.
We also received solutions from Alex and Prateek ( Riccarton High School, Christchurch, New Zealand), and Ramani (Australia). Well done to everyone.
