 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
AMGM



- Problem
- Student Solutions
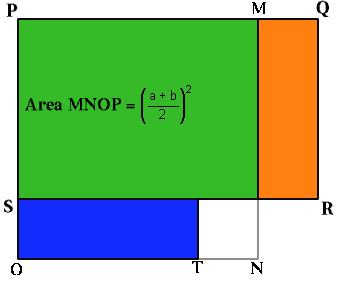
If we choose any two numbers, call them $a$ and $b$ $(b < a)$ and work out the arithmetic mean $ (a+b)/2 $ and the geometric mean $ \sqrt(ab) $ then the arithmetic mean is always bigger than the geometric mean. How can we prove it? One way is to use this diagram. Clement Goh, age 12 years, from River Valley High, Singapore sent a good solution.
In the diagram the measurements are:
PQ = a
PS = b
PM = PO = (a + b)/2
MQ = SO = TN = (a - b)/2
The blue rectangle measures (a - b)/2 by b , the same as the orange rectangle.
Rectangle PQRS, with area ab, is made up of the green plus the
orange rectangle..
The square MNOP, with area [ (a + b)/2 ] 2 , is
made up of the green plus the blue rectangles plus the yellow
square.
area of MNOP - area PQRS = the area of the yellow square = [ (a - b)/2 ] 2 .
Hence the area of PQRS < area MNOP, that is ab < [ (a + b)/2 ] 2 .
Taking square roots this shows that the geometric mean $ \sqrt(ab) $ is less than the arithmetic mean $ [(a + b)/2] $.