• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Explore further

 

The Golden Ratio

and the human body

 

This exercise is divided into 3 parts:

 

A. The golden ratio

Measure the following:

 

• Distance from the ground to your belly button

• Distance from your belly button to the top of your head

• Distance from the ground to your knees

• Distances A, B and C

• Length of your hand

• Distance from your wrist to your elbow

 

Now calculate the following ratios:

 

1. Distance from the ground to your belly button / Distance from your belly button to the top of your head

2. Distance from the ground to your belly button / Distance from the ground to your knees

3. Distance C / Distance B

4. Distance B / Distance A

5. Distance from your wrist to your elbow / Length of your hand

 

Write all your results on the following table:

 

Student name	Ratio 1	Ratio 2	Ratio 3	Ratio 4	Ratio 5
...
Average

 

Can you see anything special about these ratios?

 

B. The fibonacci sequence

 

Now look at the following sequence of numbers:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...

 

The following number is the sum of the previous two. This is Fibonacci's sequence.

 

Now do the following ratios on a calculator and give answers in non-fraction numbers:

1/2 =

3/2 =

5/3 =

8/5 =

13/8 =

21/13 =

34/21 =

55/34 =

89/55 =

 

As you go on and on dividing a number in the sequence by the previous number you get closer and closer to the number you discovered in the first part of the exercise, phi = $\phi$ = 1.6180339887498948482.

 

C. The golden rectangle

 

We can also draw a rectangle with the fibonacci number's ratio. From this rectangle we can then derive interesting shapes.

 

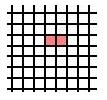
First colour in two 1x1 squares on a piece of squared paper:

 

 

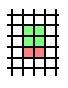
Then draw a 2x2 square on top of this one:

 

 

Then draw a 3x3 square to the right of these:

 

 

 

Then draw a 5x5 square under these:

 

 

 

 

 

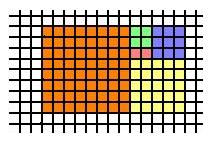
Then draw a 8x8 square to the left of these:

 

 

 

 

 

 

 

Then draw a 13x13 square on top of these:

 

 

 

 

 

 

We could go on like this forever, making bigger and bigger rectangles in which the ratio of length/ width gets closer and closer to the Fibonacci number.

 

 

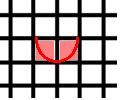Let's try making a more interesting shape, going back to our first 1x1 squares and using a compass, place the compass tip on the top right hand corner of the right hand square and draw a semi circle like this:

 

 

 

Then place the compass tip on the bottom left corner of the 2x2 square and draw an arc like this:

 

 

 

 

 

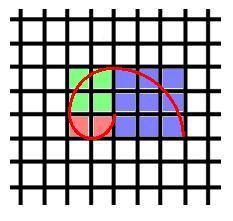
Then place the compass tip on the left hand, top corner of the 3x3 square and do the same:

 

 

 

 

Do the same for the other three squares to obtain:

 

 

 

 

 

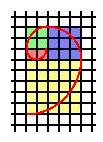
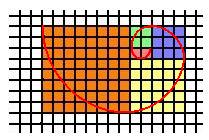
This shape is widely found in nature, can you find any other examples?