Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Pool Shot
Age 16 to 18
ShortChallenge Level 





- Problem
- Getting Started
- Solutions
We assume that the angle of incidence is equal to the angle of reflection and there is a point ball and point holes.
1) $\alpha$ could be equal to $\frac{\pi}{2}, tan^{-1}(\frac{a}{2b}), tan^{-1}(\frac{a}{3b}), tan^{-1}(\frac{a}{4b})$.
2) The suitable values of $\alpha$ could be $\frac{\pi}{2}, tan^{-1}(\frac{a}{2b}), tan^{-1}(\frac{a}{4b}), tan^{-1}(\frac{a}{8b})$.
You can check these angles by drawing diagrams. Actually there is an infinite number of possible angles.
3) In this situation we need to be careful that the ball will not go through any other hole before it goes through required one.
For the 2) case possible answers are the same.
For the 1) case use symmetry to help to understand what happens. We can add a number of pool tables like blocks and imagine that the ball is moving in a straight line. If the trajectory line goes through any point A, B, C, D, E, F it means that the ball stops at this point because it will be in the hole.
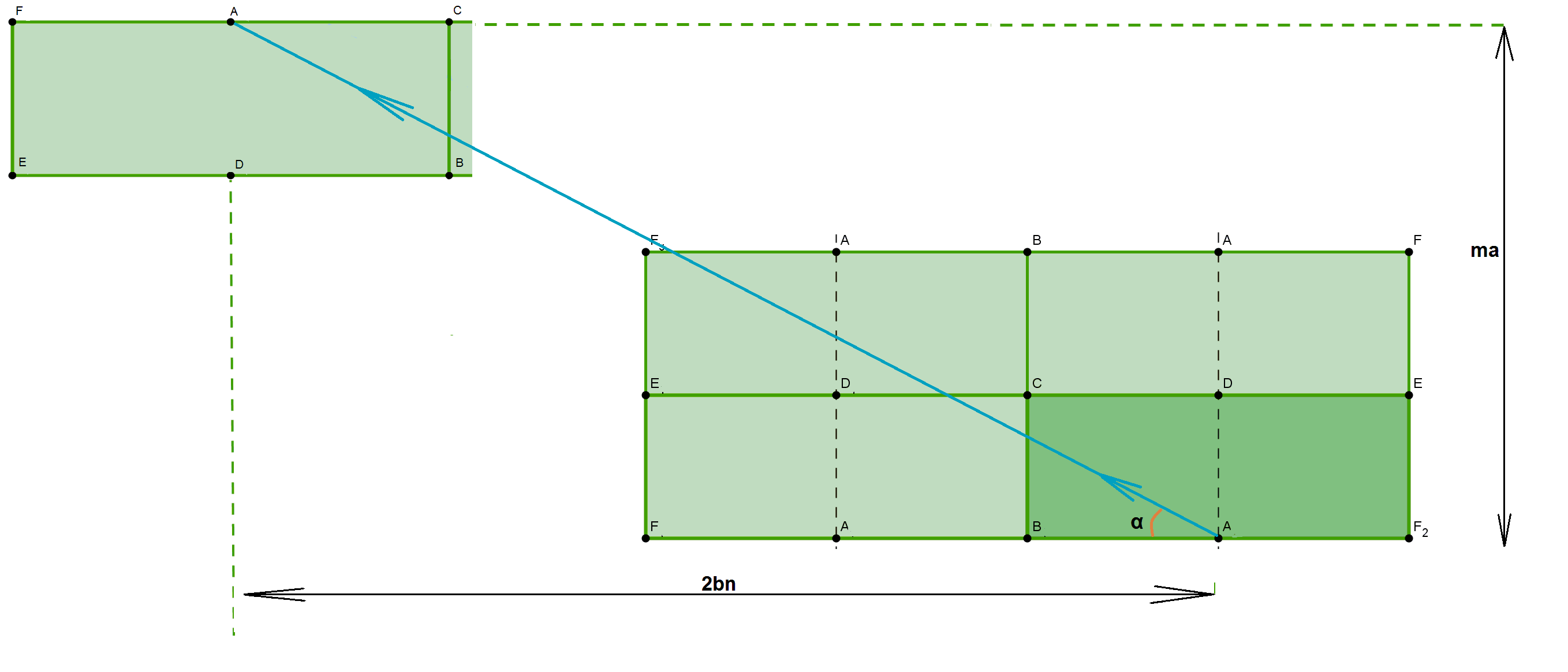
Suppose that the ball is moving along a line such that $\tan(\alpha) = \frac{ma}{2nb}$ where $m$ and $n$ are natural numbers. We see from the picture that $m$ and $2n$ must be even numbers in order for the ball to get back to a point A. Write $m = 2k$ and $2n$ is already even. $$\tan(\alpha) = \frac{2ka}{2nb} = \frac{ka}{nb}$$ Thus, we will go through the point (bn, ka). If $n$ and $k$ are both even then simplify again until you get that one of them is odd.
This means that the ball can't be hit in such a way that it will go back to the same position.
1) $\alpha$ could be equal to $\frac{\pi}{2}, tan^{-1}(\frac{a}{2b}), tan^{-1}(\frac{a}{3b}), tan^{-1}(\frac{a}{4b})$.
2) The suitable values of $\alpha$ could be $\frac{\pi}{2}, tan^{-1}(\frac{a}{2b}), tan^{-1}(\frac{a}{4b}), tan^{-1}(\frac{a}{8b})$.
You can check these angles by drawing diagrams. Actually there is an infinite number of possible angles.
3) In this situation we need to be careful that the ball will not go through any other hole before it goes through required one.
For the 2) case possible answers are the same.
For the 1) case use symmetry to help to understand what happens. We can add a number of pool tables like blocks and imagine that the ball is moving in a straight line. If the trajectory line goes through any point A, B, C, D, E, F it means that the ball stops at this point because it will be in the hole.

Suppose that the ball is moving along a line such that $\tan(\alpha) = \frac{ma}{2nb}$ where $m$ and $n$ are natural numbers. We see from the picture that $m$ and $2n$ must be even numbers in order for the ball to get back to a point A. Write $m = 2k$ and $2n$ is already even. $$\tan(\alpha) = \frac{2ka}{2nb} = \frac{ka}{nb}$$ Thus, we will go through the point (bn, ka). If $n$ and $k$ are both even then simplify again until you get that one of them is odd.
This means that the ball can't be hit in such a way that it will go back to the same position.