Consider a cube and paths along the edges of the cube.

Mark one vertex red.

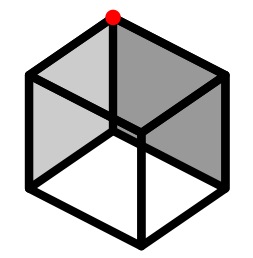
Colour other vertices red if they can be reached from a red vertex by travelling along an even number of edges of the cube.

Colour vertices blue if they can be reached by travelling along an odd number of edges from a red vertex.

Is it possible to have vertices which are both red and blue at the same time (call these redblue vertices)?

Now do the same for a tetrahedron.

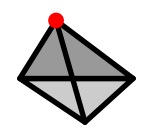
Do the same for other solids, for example the octahedron, dodecahedron and icosahedron, and prisms with different cross sections. Remember the paths must be along the edges of the solids. Decide how to record what you find. What property does the solid need if it is to have redblue vertices?