 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Family Tree



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We had several solutions to this problem. Michael explained his reasoning as below. You will probably find it easiest to follow the solution if you fill in the people on a copy of the tree as you read it.
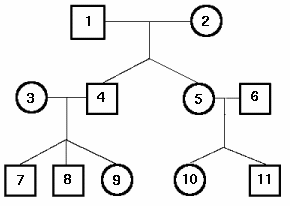
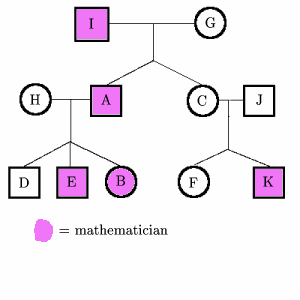
G must be $1$ or $2$ as she mentions a granddaughter; and she is
female so she is number $2$. We also know that she is a
non-mathematician. Her granddaughter, B, must be $9$ or $10$.
E, as the youngest male, must be $8$ or $11$.
J is $6$ or $3$ (if we allow 'brother-in-law' to describe her
husband's sister's husband).
F has exactly one brother, so must be $5$, $7$, $8$ or $10$.
C has a husband, and says her father is a mathematician, so C is
$5$. Therefore $1$ is a mathematician, and as the oldest
mathematician in the family can be identified as I. F can no longer
be $5$.
D, having cousins in the tree, must be one of the third
generation.
There is now no option but to assume that J is $6$. [Michael
hasn't quite explained why: he probably noticed that $6$ is C's
husband, and therefore not a mathematician, and so J can't be
$3$.] From here we can deduce that $4$ is a mathematician, and
that E and B are his children, since they have each said that their
father is a mathematician.
We can now rule out F being $7$ or $8$, and so F is $10$. F tells
us that her parents (C and J) are not mathematicians, and her
brother ($11$) is.
H is a mother of two mathematicians, so she is $3$, and either $7$
or $9$ is a mathematician (we were told that E is). This means that
for D to have just one mathematician cousin, D must be $7$ and F
must be a non-mathematician.
Finally, A must be $11$, as his father is a mathematician, so K is
$11$. We still haven't said which of $7$ and $9$ is the
mathematician, but since we haven't yet got a female mathematician,
it must be B.
Other people who sent in correct solutions (but mostly without such detailed explanation) were Claire , Sian and Fiona of Stamford High School; Ankaru; Samantha, Jacqui, Sandy and Claire of The Mount School, York; Chong Ching, Clement Goh, Chen Wei and Ng Yan; Emma and Monica of Hethersett High School, Norwich.