 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Non-transitive Dice



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We received lots of solutions to this problem with interesting strategies and ideas - well done to everyone who submitted one. Some people thought about which die Charlie is most likely to pick, and how Alison could respond. This is Johnny's work, from the British School Al Khubairat in the UAE:
So, I think that it was a bad idea for Charlie to go first, because he could pick the dice that had a 1/3 chance of being 9 (Dice B) or the dice that had a 1/3 chance of being 8 (Dice A) or the one that had a 1/3 chance of being 7(Dice C). If Charlie chose Dice B, he could potentially roll a 9, but he has a 66.6% chance of getting a much lower number. If he chooses Dice A, he has a 1 in 3 chance of rolling an 8, but again a 66.6% chance of rolling a lower number. He will probably go for Dice B, because of the high number possibility. If he does, Alison should go for Dice C, because if Charlie rolls a low number, she has a high chance of beating him, because she has 1/3 chance of 3, a 1/3 chance of 5 and a 1/3 chance of 7, which are all higher than the lowest possible number on Dice A and B.
Other people thought about what would happen with each pair of dice. For each pair, Nishtha from St Johns College Woodlawn in Australia compared the two lowest numbers, the two medium numbers and the two highest numbers. Will this always work?
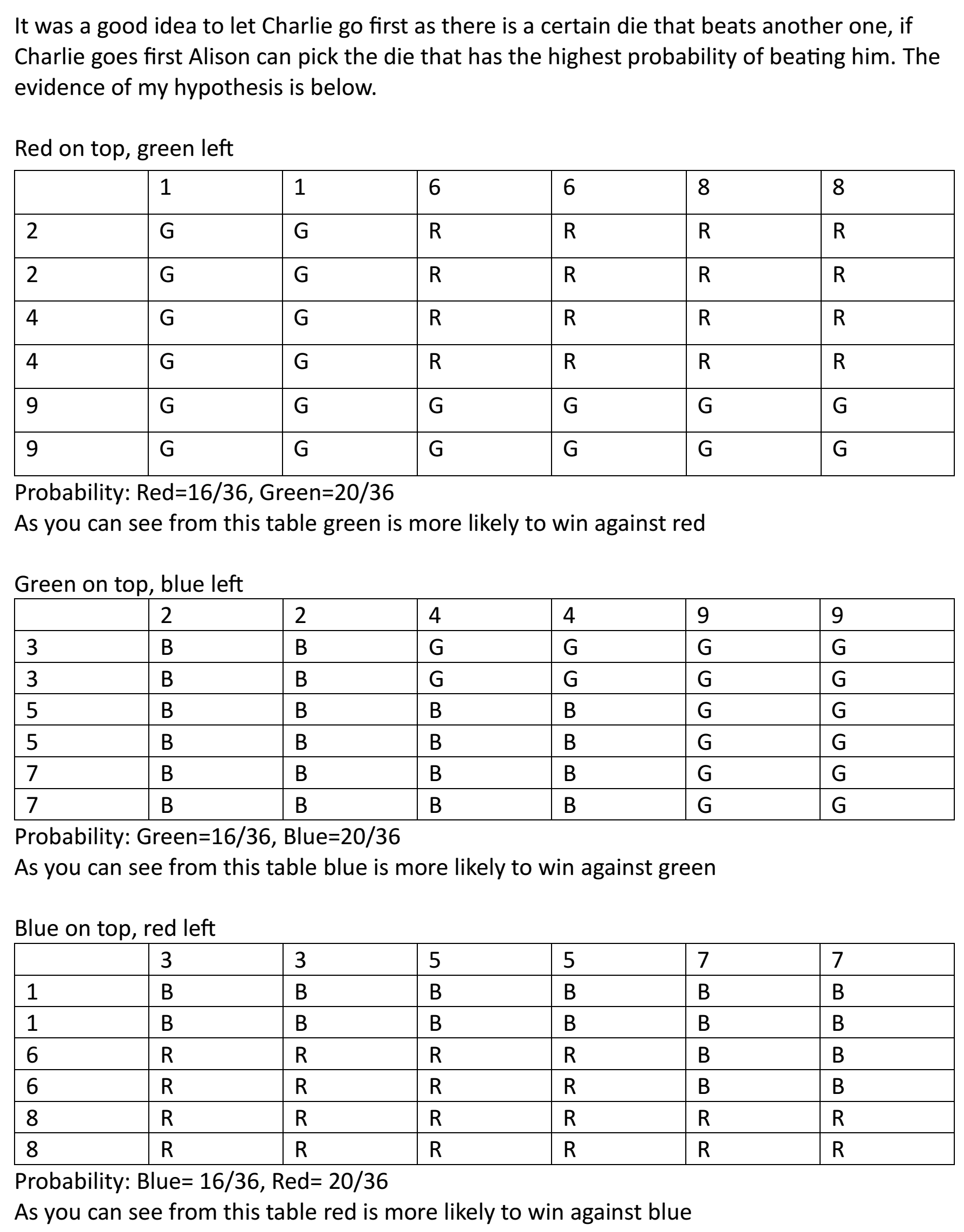
Red die- To begin with, if Player 1 picks the red die (1, 1, 6, 6, 8, 8)
Player 2 can pick green (2, 2, 4, 4, 9, 9).
Overall, green has 2/3 chances of winning
Red- 1, 1, 6, 6, 8, 8 6, 6
Green- 2, 2, 4, 4, 9, 9, 2, 2, 9, 9
If player 1 picks green instead, player 2 can pick blue, as blue has a 2/3 chance or winning, and green is left with 1/3.
Blue- 3, 3, 5, 5, 7, 7 3, 3, 5, 5, (4 points or 2/3)
Green-2, 2, 4, 4, 9, 9 9, 9, (2 points or 1/3)
Finally, if player 1 picks the blue die, player 2 can pick the red die, in
order to get the chance of 2/3 to win, and leaving player 1 with 1/3,
making them less likely to win.
Blue 3, 3, 5, 5, 7, 7 3, 3, (2 points)
Red 1, 1, 6, 6, 8, 8 6, 6, 8, 8, (4 points)
Alice from NLCS in the UK considered which numbers 'beat' which other numbers in each pairing:
For each die, there is always another die which has a higher probability of obtaining a bigger number.
For example, in the red and green die, the red die’s 6 is bigger than the green die’s 2 and 4, and the 8 is bigger than 2 and 4 too, however the green die’s 2 is bigger than 1, 4 is bigger than 1, and 9 is bigger than 1, 6 and 8. So we have the red die has 4 different ways of obtaining a bigger number, but the green die has 5 different ways obtaining a bigger number, so the green die is more likely to win.
Egan from Marymount London and Yuhan from St George's British International School, Rome also counted how many ways each die could win in each pairing. Egan showed this as a table. Here is Egan's work:
Andrew from Kellet School in Hong Kong, Annabella from St George's British International School, Rome and Ci Hui Minh Ngoc Ong from Kelvin Grove State College Brisbane in Australia all used a similar idea, but expressed their work in probabilities on tree diagrams. Here is Andrew's work:
Lucas and Juan from Kellett School in Hong Kong also paired the dice up against each other, but then tried a very different approach. They simulated games between each pair of dice. They did these simulations in Desmos - randomised trials on Desmos. This is their work (click on the image to open a larger version):

