Why do this problem?

Working on this problem will give students a deeper understanding of the relationship between volume and surface area, and how they change as the dimensions of a cuboid are altered.

Possible approach

This problem follows on from Changing Areas, Changing Perimeters. We suggest students start with the rectangles task from that problem to introduce them to the structure of the grid they will be using here.

 

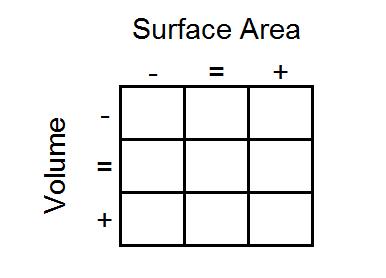
For those who finish quickly, ask them the question from the problem about extending the grid like this:
 

Towards the end of the lesson, bring the class together to share any efficient strategies they used to complete the task.
 
Pose the question "If I know two cuboids have the same volume, how can I decide, just by looking at their dimensions, which has the greater surface area?"

Draw out students' ideas about the properties of long and thin cuboids as opposed to those that are almost cubes.
(This is the three dimensional analogue of short and fat rectangles having a smaller perimeter than long thin ones, when their areas are equal.)
 
Finally, discuss the possible content of the four extra spaces in the extended grid and strategies they used to generate possibilities.

Possible support

Changing Areas, Changing Perimeters provides a two-dimensional version of this three-dimensional problem.
 

Possible extension

Challenge students to design their own set of nine cards that can be arranged in this way. If students are restricted to whole numbers it is quite challenging to create cuboids with equal surface areas.