 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Changing Areas, Changing Volumes



This problem follows on from Changing Areas, Changing Perimeters.
Changing Areas, Changing Volumes printable sheet
Here are the dimensions of nine cuboids. You can download a set of cards here.
|
1 by 2 by 28
cuboid
|
4 by 4 by 4
cube
|
2 by 4 by 7
cuboid
|
|
1 by 2 by 26
cuboid
|
2 by 4 by 6
cuboid
|
4 by 5 by 6
cuboid
|
|
4 by 5 by 7
cuboid
|
1 by 2 by 24
cuboid
|
1 by 4 by 14
cuboid
|
The challenge is to arrange them in a 3 by 3 grid like the one below:
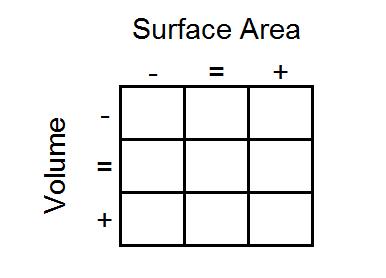
As you go from left to right, the surface area of the shapes must increase.
As you go from top to bottom, the volume of the shapes must increase.
All the cuboids in the middle column must have the same surface area.
All the cuboids on the middle row must have the same volume.
What reasoning can you use to help you to decide where each cuboid must go?
Once you've placed the nine cards, take a look at the extended grid below:
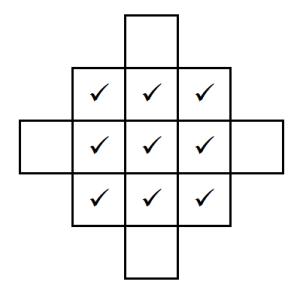
The ticks represent the nine cards you've already placed. Can you create cards with dimensions for cuboids that could go in the four blank spaces that satisfy the same criteria?
Can you design a set of cards of your own with a different cuboid in the centre?