Changing Areas, Changing Perimeters

'Changing Areas, Changing Perimeters' printed from https://nrich.maths.org/

Show menu

Changing Areas, Changing Perimeters printable sheets: Instructions, Shapes, Dimensions

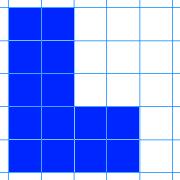
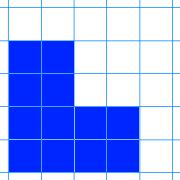
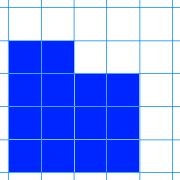
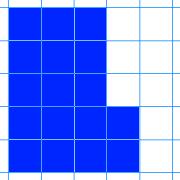
Here are nine shapes. You can download a set of these shapes to print off here.

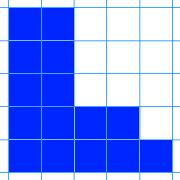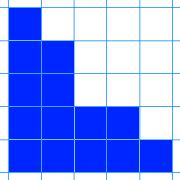The challenge is to arrange the shapes in a 3 by 3 grid like the one below:

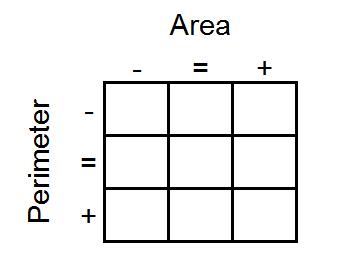
As you go from left to right, the area of the shapes must increase.
As you go from top to bottom, the perimeter of the shapes must increase.
All the shapes in the middle column must have the same area.
All the shapes on the middle row must have the same perimeter.

What reasoning can you use to help you to decide where each card must go?

Here are the dimensions of nine rectangles (printable version here).

$2$ by $8$ rectangle	$4$ by $4$ square	$1$ by $15$ rectangle
$5$ by $5$ square	$3$ by $8$ rectangle	$2$ by $7$ rectangle
$1$ by $16$ rectangle	$3$ by $6$ rectangle	$1$ by $9$ rectangle

Can you arrange them in the grid in the same way?

Once you've placed the nine cards, take a look at the extended grid below:

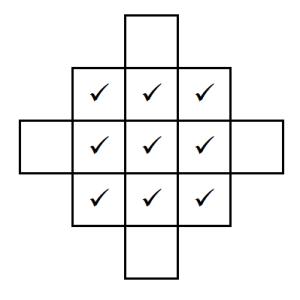
The ticks represent the nine cards you've already placed.
Can you create cards with dimensions for rectangles that could go in the four blank spaces that satisfy the same criteria?
Not all the spaces are possible to fill. Can you explain why?

Can you produce a set of cards that could be arranged in the same way, if the card in the centre is a 1 by 5 rectangle?