Thank you to everybody who sent in their solutions to this problem. We received a lot of correct solutions and lots of children said that they had worked systematically to make sure that they found all the solutions - well done to all of you! Only a few children explained how they did this, so we've focused on those solutions here.

Beth from Halstead Preparatory School in England said:

My solutions were:
8, 7, 13, 10, 6, 12, 9
6, 9, 11, 12, 4, 14, 7

The way I did this was I added all the numbers to 15, 20, 23, 16, 18, and 21 and then I tried all the solutions until I found them all.

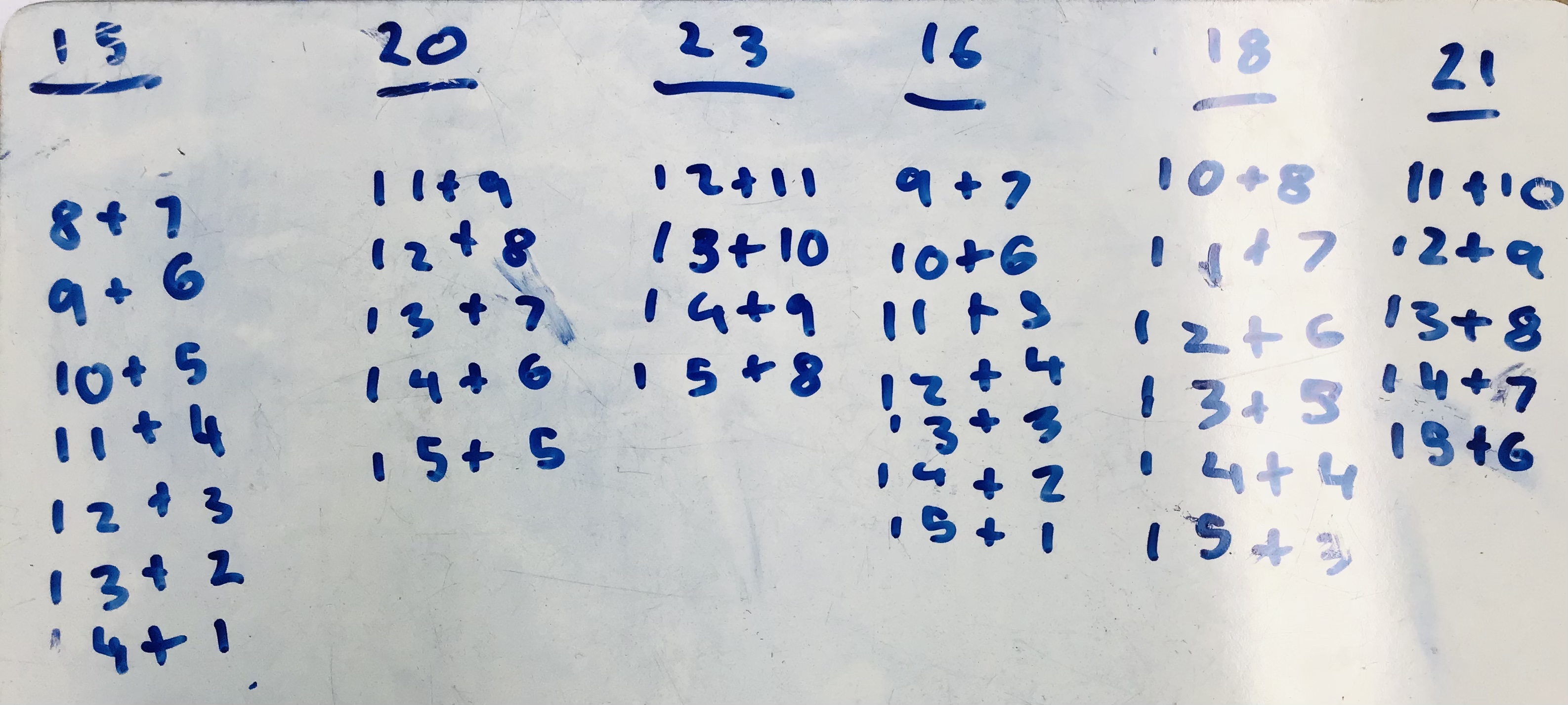
This is a really clear table, Beth - I'm convinced that you've looked at all of the possibilities here. I wonder how Beth used this table to find the different solutions?

Aanya, also from Halstead, showed us how they began to answer the question:

I worked out this problem by using trial and error in a systematic way.
This is how I did it.

1+14=15. 14+6=20. 6+17=23. You can’t use 17.
14+1=15. 1+19=20. You can’t use 19.
2+13=15. 13+7=20. 7+16=23. You can’t use 16.
13+2=15. 2+18=20. You can’t use 18.

Good start, Aanya! What would Aanya have done next using this method?

We were sent a few solutions that showed us the systematic working to check every possible combination of cards. Anahita from Woodford Green Preparatory School in the UK sent us this picture:

Maymanah from Herringthorpe Junior School sent in a very similar description and explanation:

1, 14, 6, 17 X
2, 13, 7, 16 X
3, 12, 8, 15, 1, 17 X
4, 11, 9, 14, 2, 16 X
5, 10, 10 X
6, 9, 11, 12, 4, 14, 7 Correct!
7, 8, 12, 11, 5, 13, 8 X
8, 7, 13, 10, 6, 12, 9 Correct!
9, 6, 14, 9 X
10, 5, 15, 8, 8 X
11, 4, 16 X
12, 3, 17 X
13, 2, 18 X
14, 1, 19 X
15, 0 X

First, I started with 1 as the first card, but I realised that I couldn't start with 1 or 2 as some cards required a number more than 15 so I continued with 3 and onwards. I realised that it couldn't be 5 as the first card because that needed repeat number 10 cards. Then I got up to 6 and it worked all the way through. Then I carried on from 7 to see if I could find any more solutions. Then I came across 8 and found another answer! After that I carried on looking for any other answers. When I got to 11, I realised that there were no more answers as some cards need more than 15. That is how I worked out the question.

Thank you both for sharing your working with us! I wonder if there are any patterns you can spot in the full solutions, looking at the possibilities that don't work as well as the ones that do. Why do these patterns happen?

We were also sent in some other solutions that explained how they worked systematically to find the answers. Well done to: all the children in Cherry Class at Bramfield Primary School in England; Viren KS; Dhruv from The Glasgow Academy in the UK; Mia, Jolene, May and Joanna from Falcons School for Girls; and Hiren, Vansh, Eshaan, Rishaan, Samaira, Renah, Udit, Uday, Viha, Gowri, Arya, Vishnu, Krishna, Rivaan, Miraya from Ganit Kreeda in India.

Ci Hui Minh Ngoc from Kelvin Grove State College in Brisbane, Australia used algebra to find all the possible solutions:

Well done, Ci Hui Minh Ngoc! This is a similar idea to the one Maymanah described, where you can narrow down the possibilities for the first card before working out all the possible solutions.