Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Walking the Squares
Age 7 to 11
Challenge Level 





- Problem
- Student Solutions
- Teachers' Resources
Walking the Squares
So here's a special square of tiles to walk on!

The black square in the middle contains some very special prizes.
You can get the prizes by collecting tokens which are on each tile. So you have to step on as many tiles as possible.
BUT
You cannot go onto any tile more than once.
You are not allowed to step on more than two tiles of the same colour one after another.
So this path would be OK.
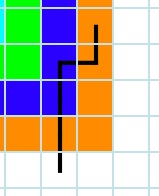
But this path is not allowed;
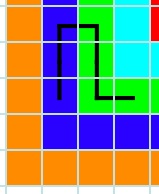
Why? Because the path goes along $3$ blues which is not allowed, the blue to green is OK but then tere are $4$ green tiles one this path next to each other and that is also not allowed.
Your challenge is to find a path from anywhere on the outside of the square to the black square in the middle, following the rules above and trying to step on as many tiles as possible.
Your challenge is to find a path from anywhere on the outside of the square to the black square in the middle, following the rules above and trying to step on as many tiles as possible.
Why do this problem?
This activity gives pupils an opportunity to explore a scenario and gradually start using a strategy while learning to overcome difficulties. It also gives pupils an opportunity to use their curiosity to pursue many different associated questions. Their perseverance can be tested alongside their resilience in answering their own questions
of "I wonder what would happen if we . . .?
Possible approach
It would be good to give pupils a sheet with several copies of the square on it (see here for doc or pdf).
The pupils can then work on the first one. If (and when!) they come to a stop because they realise it is going wrong, encourage them not to rub it out but write about what they are thinking - in particular what they did and what they should now do - on the right and start again underneath.
Key questions
Tell me about what happened here that made you start again.
You seen to be using a system (if it looks like it!) can you tell me about it?
Is there anything you would like to change about the way that you did it?
Have you covered as many pairs as possible?
Possible extension
Here is a page (doc, pdf) that gives you an opportunity to print out four different sizes of squares for the pupils to have a go at and compare, and perhaps then they can be encouraged to make some predictions.
Possible support
Some pupils might want to use some drawing software.