Copyright © University of Cambridge. All rights reserved.
'Factorising with Multilink' printed from https://nrich.maths.org/
Show menu
Luke from London Oratory School explained how the situation can be shown using algebra:
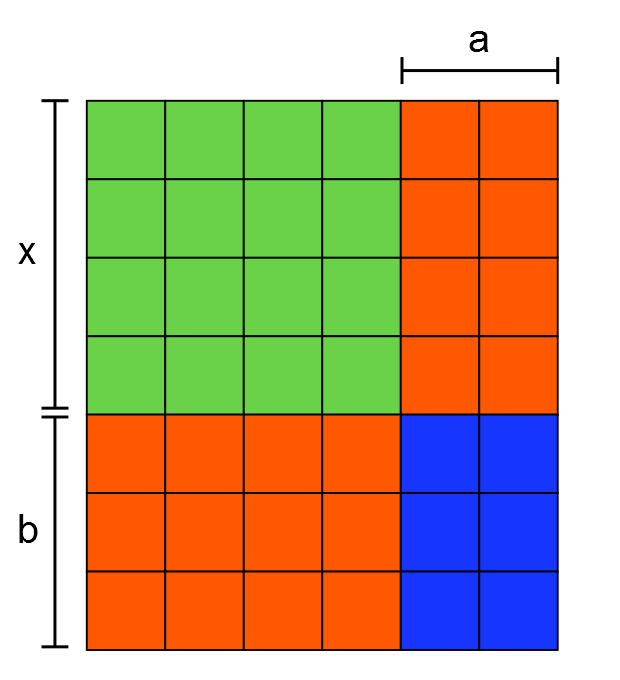
The red section (made of sticks) consists of two rectangles with dimensions $a, x$ and $b, x$. Therefore the red area is equal to $ax+bx$, which equals $x(a+b)$.
We can see that the area of the blue section will always have dimensions $a$ and $b$, so its area is equal to $ab$, if it Ê»ï¬llsʼ the gap created by the red area.
The total area is equal to the sum of these component areas.
Thus you can make a rectangle for all bases for expression of the form $x^2 + x(a+b) + ab$ where $a$ and $b$ are positive integers. The rectangle has dimensions $(x+a)$ by $(x+b)$.
1 square, lots of sticks and 12 or 100 units
Mahdi, Hamaad and Khalid used algebra again. Here is Mahdi's work for 12 sticks:
This is Hamaad and Khalid's work for 100 sticks:
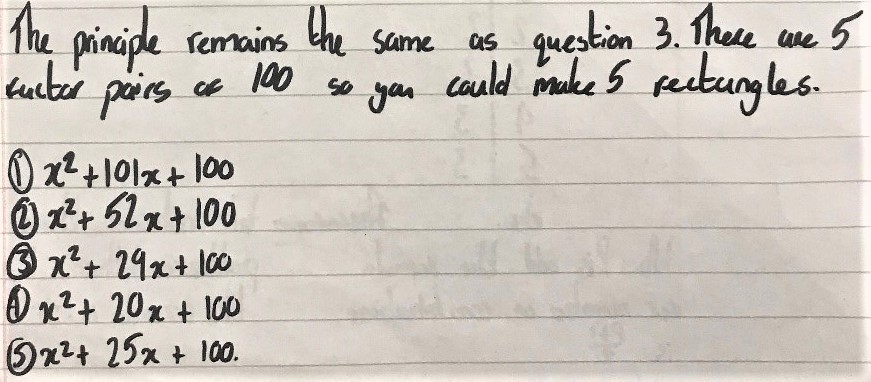
1 square, 12 or 100 sticks and lots of units
Hadi from Michaela Community School in the UK started with smaller numbers of sticks and then spotted a pattern:
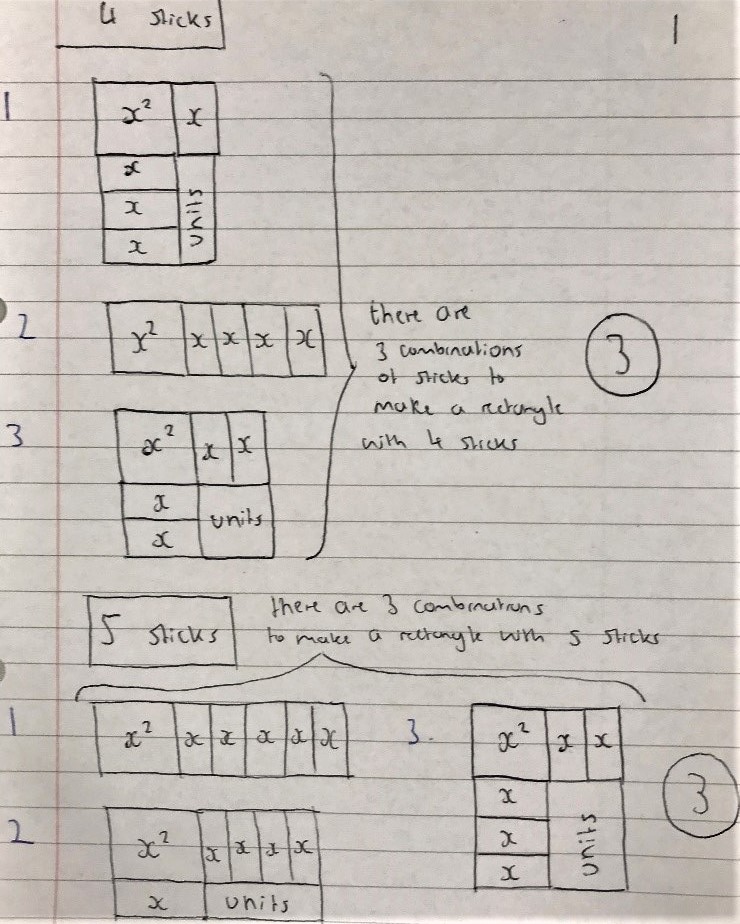
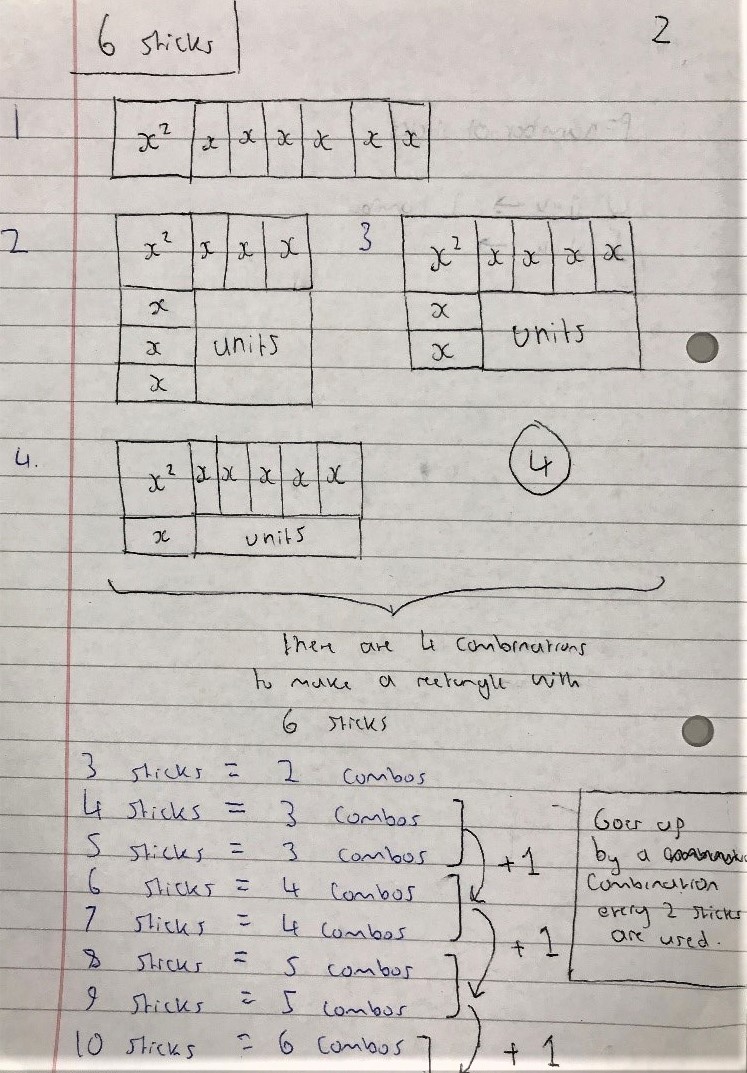

Mahdi from Mahatma Gandhi International School in India used algebra:
Hamaad and Khalid from Michaela Community School and Mahdi used the same approah for 100 sticks. This is Hamaad and Khalid's work:

For $p$ sticks and $q$ units
Mahdi approached this algebraically:
So how many different rectangles can you make with $p$ sticks and $q$ units?