Copyright © University of Cambridge. All rights reserved.
'Stand up Arcs' printed from https://nrich.maths.org/
Show menu
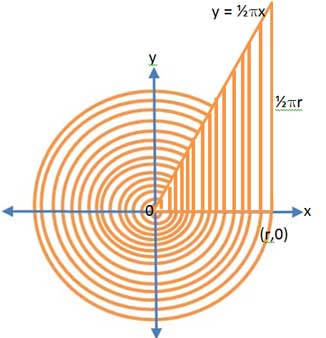
Imagine the circle filled with infinitely many concentric rings.
Now focus on the first quadrant. Imagine straightening all the quarter circles into vertical strips. Why do all the tops of the strips lie on the line $y = \frac{1}{2}\pi x$? Remember there are infinitely many strips so they fill a triangular area as shown in the diagram.
Why is it that the arcs are not stretched in this process, only straightened, so that the area of each strip stays the same when you straighten each arc into a straight line?
What does this tell you about the area of the circle?
The 'strings' could be longer. Suppose instead of straightening quarter circles you straightened arcs which were whole circles. Then on what line would the tops of the straight 'stand up arcs' lie? Again the area of the triangle packed with strips made of straightened arcs of circles is equal to the area of the circle and this gives the formula for the area of the circle.
Did you know ... ?
Radians are a more natural measure for angles than degrees. One radian is the angle subtended at the centre of a circle by an arc that is equal in length to the radius of the circle. The length $s$ of an arc is proportional to the radius $r$ and also to the angle $\theta$ that the arc subtends at the centre of the circle, that is $s = r\theta$. It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or $\frac{2\pi r }{r}$ or $2\pi$. Thus $2\pi$ radians is equal to 360 degrees, meaning that one radian is equal to $\frac{180}{\pi}$ degrees.
Radians are a more natural measure for angles than degrees. One radian is the angle subtended at the centre of a circle by an arc that is equal in length to the radius of the circle. The length $s$ of an arc is proportional to the radius $r$ and also to the angle $\theta$ that the arc subtends at the centre of the circle, that is $s = r\theta$. It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or $\frac{2\pi r }{r}$ or $2\pi$. Thus $2\pi$ radians is equal to 360 degrees, meaning that one radian is equal to $\frac{180}{\pi}$ degrees.