Little and large
A point moves around inside a rectangle. What are the least and the
greatest values of the sum of the squares of the distances from the
vertices?
Age
16 to 18
Challenge level
Problem
Image
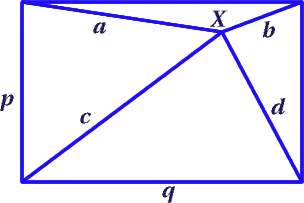
The point $X$ moves around inside a rectangle of dimension $p$ units by $q$ units. The distances of $X$ from the vertices of the rectangle are $a$, $b$, $c$ and $d$ units. What are the least and the greatest values of
$a^2 + b^2 + c^2 + d^2$
and where is the point $X$ when these values occur?
Student Solutions
Congratulations to Soh Yong Sheng from Raffles Institution,
Singapore for this excellent solution.
We have $0 < a < b$ which means $1/a > 1/b$ and so $3 + 1/a > 3 + 1/b$. Flipping over the fraction, we will get 1/(3 + 1/a) < 1/(3 + 1/b) and the inequality remains the same way round when 2 is added. Flipping over again for the last time we get
The second part is a further expansion of the first, and in the process of repeating the above we know that it involves just one more flipping over of the fraction, thus
Lastly the continued fractions are expanded all the way down to $100 + 1/a$ and $100 + 1/b$. Observe the above process, we can tell that if the last or biggest number is odd then the continued fraction with a in it is bigger. If the last or biggest number is even then the continued fraction with $b$ in it is bigger. Each successive continued fraction involves one more 'flipping over' and reverses the inequality one more time. The following continued fraction is smaller than the same thing with $b$ in place of $a$:
We have $0 < a < b$ which means $1/a > 1/b$ and so $3 + 1/a > 3 + 1/b$. Flipping over the fraction, we will get 1/(3 + 1/a) < 1/(3 + 1/b) and the inequality remains the same way round when 2 is added. Flipping over again for the last time we get
The second part is a further expansion of the first, and in the process of repeating the above we know that it involves just one more flipping over of the fraction, thus
Lastly the continued fractions are expanded all the way down to $100 + 1/a$ and $100 + 1/b$. Observe the above process, we can tell that if the last or biggest number is odd then the continued fraction with a in it is bigger. If the last or biggest number is even then the continued fraction with $b$ in it is bigger. Each successive continued fraction involves one more 'flipping over' and reverses the inequality one more time. The following continued fraction is smaller than the same thing with $b$ in place of $a$: