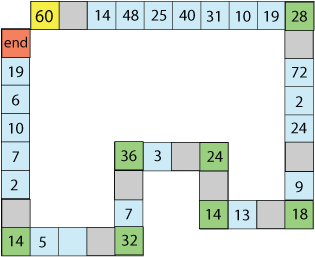
Factor track
Factor track is not a race but a game of skill. The idea is to go round the track in as few moves as possible, keeping to the rules.
Problem
Factor Track is not a race but a game of skill.
Below is a simple training version. The idea is to go round the track in as few turns as possible, keeping to the rules.

For accessibility, clicking on the 'image description' button below will show a description of this image.
Image description
The track consists of straight lines of squares that are either blank or have numbers in. The straight lines of squares are joined by corner squares.
Start: 60
Blank
14
48
25
40
31
10
19
Corner: 28
Blank
72
2
24
Blank
9
Corner: 18
Blank
13
Corner: 14
Blank
Corner: 24
Blank
3
Corner: 36
Blank
7
Corner: 32
Blank
Blank
5
Corner: 14
Blank
2
7
10
6
19
End
Rules:
You start on the 'Start' square and must make your way round to the 'End' square.
You can move any factor of the number you are on, except 1.
You must land exactly on each corner (green) square, so you can't go round corners in one turn.
Have a go at moving round this 'training' track following the rules.
Can you do it in fewer turns?
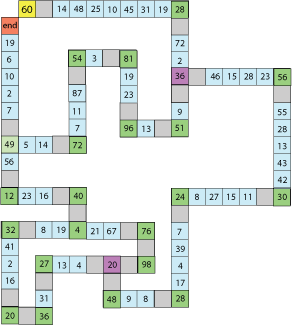
When you feel ready, try this more complicated track where there are possible short cuts. You will have to work out whether they are worthwhile. You can click on this image to make it bigger.

For accessibility, clicking on the 'image description' button below will show a description of this image.
Image description
The track consists of straight lines of squares that are either blank or have numbers in. The straight lines of squares are joined by corner squares.
Start: 60
Blank
14
48
25
10
45
31
19
Corner: 28
Blank
72
2
Three-way corner A: 36
Blank
46
15
28
23
Corner: 56
Blank
55
28
13
43
42
Corner: 30
Blank
11
15
27
8
Corner: 24
Blank
7
39
4
17
Corner: 28
Blank
8
9
Corner: 48
Blank
Three-way corner B: 20
Blank
4
13
Corner: 27
Blank
31
Corner: 36
Blank
Corner: 20
Blank
16
2
41
Corner: 32
Blank
8
19
Three-way corner C: 4
Alternate route from B to C:
Three-way corner B: 20
Blank
Corner: 98
Blank
Corner: 76
Blank
67
21
Three-way corner C: 4
Blank
Corner: 40
Blank
16
23
Corner: 12
Blank
56
Three-way corner D: 49
Alternate route from A to D:
Three-way corner A: 36
Blank
9
Corner: 51
Blank
13
Corner: 96
Blank
23
19
Corner: 81
Blank
3
Corner: 54
Blank
87
11
7
Corner: 72
Blank
14
5
Three-way corner D: 49
Blank
7
2
10
6
19
End
You might find it easier to print out this larger copy of the track which also has the rules on it.
You can do this on your own or with a friend. Who can get round in the least number of turns?
What is the best route to take to do it in the least number of turns?
Which squares do you need to land on?
Printable NRICH Roadshow resource.
Getting Started
You might try writing down all factors of the numbers in the green squares.
How will you know which routes you have tried?
Student Solutions
J Darcy from Pulner Junior School and Otto completed the first Factor Track in the following 9 moves:
Divide 60 by 2 and move on 2 spaces, then divide 14 by 7 and move on 7 spaces. 7 is a factor of 28 so move on 7 spaces. 18 divides into 3 so move on 3 spaces. 14 divides into 2 so move on 2 spaces. 24 divides into 3 so move to 36. 36 divides into 3 to move to 32. 32 divides by 4 so move to 14. 14 divides by 7 to reach the end!
Lots of you went straight to the more challenging one and managed it in 10 moves including students from Wilson's School, St Helen's C of E Primary School, Baston C of E Primary School, MacDiarmid Primary School and Highfield School.
Ultra Violet Class from Unicorn explain their solution here:
Issy, Laura and Anna worked as a team to solve this problem. They found that doing the training track gave them a very good understanding of the problem. On the more complicated track they found the shortest route involved 10 steps. They used a counter and recorded each step by writing the sequence of numbers linked by arrows with the number of moves written above:
60 (3 moves) 48 (6 moves) 28 (7 moves) 51 (3 moves) 96 (4 moves) 81 (3 moves) 54 (2 moves) 87 (3 moves) 72 (4 moves) 49 (7 moves) END
They noted that the only point they could not go from corner to corner was on the first row where they had to use 2 moves between the numbers but there were lots of options:
60 to 14 to 28
60 to 48 to 28
60 to 25 to 28
60 to 45 to 28
They found using divisibility rules to check for factors of the larger numbers a very useful approach. The most helpful one being the divisibility rule for the number 3.
Alex, Jack and Jamie also came up with the shortest route of 10 steps. Peter, Ben and Jack all tried going the longer route and found they could do it in 18, 17 and 16 steps. The shortest route of 16 steps was achieved by moving from corner to corner in all but two cases. This was the first row as described above and the very last column where they had to go 12 to 49 to END.
Mr Bouchard's Class from Richmon Elementary School, USA, sent us a picture of their solution:

And Krystov's explanation can be found here.
Students from Greenacre School for Girls decided to make their own Factor Tracks. See if you can complete them.
1 by Erica and Helena
2 by Grace and Katie
3 by Rebecca and Elizabeth
4 by Rosie
5 by Sophie, Esme and Josie
6 by Zoe and Rachel
Teachers' Resources
Why do this problem?
This problem will help to improve learners' knowledge of factors, especially those in the usual multiplication tables, and encourages them to use trial and improvement. The competitive element can bring out the best in some pupils.
Possible approach
You could start by showing the group the 'training track' given in the problem, working on this so that they are able to see the rules in action. Once they have had a go, you could spend a short time discussing the reasons for their choices and ultimately the minimum number of turns that will take you round the track.
Key questions
Possible extension
Learners could make their own 'factor track' for others to try. Alternatively, the problem Factor-multiple Chains offers another interesting way to explore factors.
Possible support
You could suggest that learners record all factors of the number in green squares so they are able to keep track of the ones they have tried more easily. The problem Jumping Squares has the same idea of getting round a track in as few turns as possible but focuses on counting, rather than factors.