Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Irrational Arithmagons
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to everyone who sent a solution - we had a wonderful variety of creative solutions to this problem!
Ed from Wyoming Valley West in the USA mostly used a trial method:
I first created a system of equations rigorously:
$$\begin{align}\left( a + b \sqrt{2} \right) \times \left(c + d \sqrt{2} \right) &= -6 + 2\sqrt{2}\\
\left(a + b\sqrt2\right) \times \left(e + f\sqrt2\right) &= 2 - 4\sqrt2\\
\left(c + d\sqrt2\right) \times \left(e + f\sqrt2\right) &=7 + 7\sqrt2\end{align}$$
To get a set of 6 equations for 6 unknown variables:
$$\begin{align}ac + 2bd &= -6\\
bc + ad & = 2\\
ae + 2bf &= 2\\
be + af &= -4\\
ce + 2df& = 7\\
de + cf &= 7\end{align}$$ My matrix background is shaky at best, so while I know creating a matrix would net a unique solution, I was certain I'd make a math error along the way, so I tried instead to deduce some things logically.
First I noted that from equation 5, both $c$ and $e$ must be odd.
Then, from equation 6, either $d$ is odd and $f$ is even, or vice versa.
Then I took a leap of faith that for all these sums to be bounded by $-6$ and $7$, all 6 values should be fairly small. And since equations 5 and 6 are both positive sums, all coefficients are likely positive as well.
From that, I tried a couple guesses, but then I hit paydirt with $c=1$, $d=2$, $e=3$, $f=1.$
Once I managed success from that combination, I tested it back into equations 1 & 2.
This yielded 2 equations with only 2 unknown variables, a much more manageable task.
Equation 1 became $a + 4b = -6$
and Equation 2 became $2a + b = 2$
resulting in $a = 2$ and $b = -2$.
I checked that result into equations 3 & 4, and everything checked on the math, but to make sure I didn't violate any rules of algebra, I checked the arithmagon and the math worked out nicely.
Jamie from BSB in the UK began by considering a simpler version of the problem to find a sensible method:
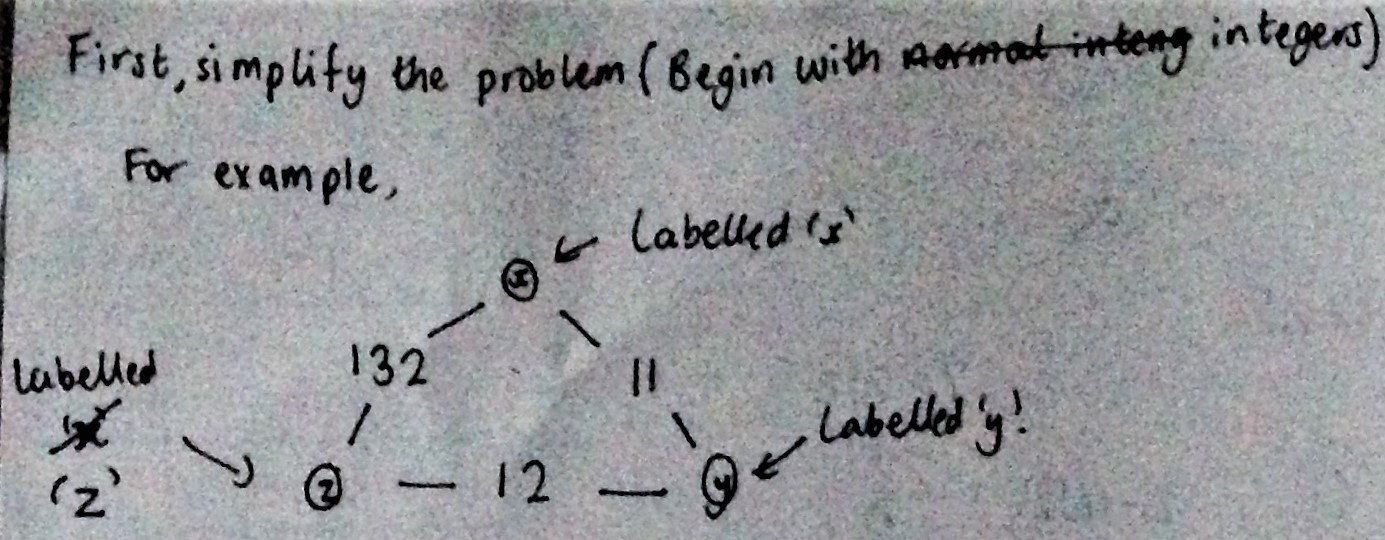
Next, set up a system of equations: $$\begin{align}xz&=132\hspace{20mm}&(1)\\xy&=11&(2)\\yx&=12&(3)\end{align}$$
from $(1)$ $z=\frac{132}x$ from $(2)$ $y=\frac{11}{x}$ from $(3)$ $y=\frac{12}z$
$\therefore \frac{11}x=\frac{12}z$
but $z=\frac{132}x$, so $\frac{11}x=\frac{12x}{132}$
and so $\frac{11\times132}{12}=x^2$
By repeating this process you can also find that $y^2=\frac{11\times12}{132}$ and $z^2=\frac{132\times12}{11}$
Jamie went on to apply this method to the problem:
From our previous research of multiplication arithmagons, we can deduce that $$\begin{align}b^2&=\frac{\left(7+7\sqrt2\right)\left(2-4\sqrt2\right)}{-6+2\sqrt2}\\
&=\frac{14-28\sqrt2+14\sqrt2-28\times2}{-6+2\sqrt2}\\
&=\frac{-14\left(3+\sqrt2\right)}{-2\left(3-\sqrt2\right)}\\
&=\frac{7\left(3+\sqrt2\right)\left(3+\sqrt2\right)}{\left(3-\sqrt2\right)\left(3+\sqrt2\right)}\\
&=\frac{7\left(9+6\sqrt2+2\right)}{9-2}\\
&=11+6\sqrt2\end{align}$$ $\left(11+6\sqrt2\right)$ can be expressed $\left(x+y\sqrt2\right)^2$ to allow for the square rooting of $b^2$. $$\begin{split} 11+6\sqrt2&=\left(x+y\sqrt2\right)^2\\&=x^2+2y^2+2xy\sqrt2\end{split}$$ Form simultaneous equations $$\begin{align}x^2+2y^2&=11\hspace{20mm}&(1)\\
2xy\sqrt2&=6\sqrt2&(2)\end{align}$$
From $(2)$, $2xy=6$ so $x=\frac3y$.
We can substitute this into $(1)$: $$\begin{align}x^2+2y^2&=11\\
\left(\frac3y\right)^2+2y^2&=11\\
\Rightarrow\frac{9+2y^4}{y^2}&=11\\
\Rightarrow2y^4-11y^2+9&=0\\
\Rightarrow(2y^2-9)(y^2-1)&=0\end{align}$$ Ignore $2y^2-1=0$ since $y$ should be an integer. If $y^2-1=0$ then $y=1$ or $y=-1$.
But $x=\frac3y$, so $x=3$ or $x=-3$ So $b=\pm\left(3+\sqrt2\right)$ $$\begin{align} ab&=7+7\sqrt2\\
\Rightarrow a&=\frac{7+7\sqrt2}{b}\\
\Rightarrow a&=\frac{7+7\sqrt2}{3+\sqrt2}\end{align}$$ Now, rationalise the denonimator $$\begin{align}a&=\frac{\left(7+7\sqrt2\right)\left(3-\sqrt2\right)}{\left(3+\sqrt2\right)\left(3-\sqrt2\right)}\\
\Rightarrow a&=\frac{21-7\sqrt2+21\sqrt2-14}7\\
\Rightarrow a&=\frac{7+14\sqrt2}7\\
\Rightarrow a&=1+2\sqrt2\end{align}$$ So $a=\pm\left(1+2\sqrt2\right)$
Now repeat for $c$.
Kryštof from The English College in Prague used the same method as Jamie, but without doing the 'research' first. This is Kryštof's work:
First we begin by assigning variables to the vertices of the triangle, $x$, $y$ and $z$ starting at the top and going clockwise.
Then we construct a system of three equations: $$\begin{align} xy&=7+7\sqrt{2}\hspace{20mm}&(1)\\
yz&=2-4\sqrt2&(2)\\
zx&=-6+2\sqrt2&(3)\end{align}$$ The method we will use is to make $y$ the subject of equation $(1)$ and $z$ the subject of equation $(3).$ Then we will substitute into equation $(2)$ to solve for $x$. $$\begin{align}y&=\frac{7+7\sqrt2}{x}\hspace{20mm}&(4)\\
z&=\frac{-6+2\sqrt2}{x}&(5)\end{align}\\$$
$$\begin{align}\frac{7+7\sqrt2}x.\frac{-6+2\sqrt2}x&=2-4\sqrt2\\
\Rightarrow\frac{\left(7+7 \sqrt {2}\right).(-6 +2 \sqrt {2})} {2-4 \sqrt {2}} &= x^2\end{align}$$ Kryštof then found $x$ using a calculator, but could have used Jamie's method shown above, or the method that Theodore uses below.
Theodore from Institut Saint-Lô in France and Mitali from Delhi Public School Sushant Lok in India both used a very neat method. This is Theodore's working.
We have:$$\begin{align} xy&=7+7\sqrt{2}\hspace{20mm}&(1)\\
yz&=2-4\sqrt2&(2)\\
zx&=-6+2\sqrt2&(3)\end{align}$$
$$\begin{align} \Rightarrow xy\times zx&=\left(7+7\sqrt2\right)\left(-6+2\sqrt2\right)\\
\Rightarrow x^2(yx)&=-42+14\sqrt2-42\sqrt2+28\\
&=-14-28\sqrt2\\
\Rightarrow x^2\left(2-4\sqrt2\right)&=-\left(14+28\sqrt2\right)\\
\Rightarrow x^2&=-\frac{14+28\sqrt2}{2-4\sqrt2}=-\frac{14\left(1+2\sqrt2\right)}{2\left(1-2\sqrt2\right)}\\
&=\frac{-7\left(1+2\sqrt2\right)^2}{1-8}=\left(1+2\sqrt2\right)^2\end{align}$$ Hence $x=1+2\sqrt2$
$$\begin{align}zx&=-6+2\sqrt2\\
\Rightarrow z&=\frac{-6+2\sqrt2}{1+2\sqrt2}=\frac{\left(-6+2\sqrt2\right)\left(1-2\sqrt2\right)}{1-8}\\
&=\tfrac{1}{-7}\left(-6+12\sqrt2+2\sqrt2-8\right)=\tfrac{1}{-7}\left(-14+14\sqrt2\right)=2-\sqrt2\end{align}$$
$$\begin{align}xy&=7+7\sqrt2\\
\Rightarrow y=&\frac{7+7\sqrt2}{1+2\sqrt2}=\frac{\left(7+7\sqrt2\right)\left(1-2\sqrt2\right)}{1-8}\\
&=-\tfrac17\left(7-14\sqrt2+7\sqrt2-28\right)=-\tfrac17\left(-21-7\sqrt2\right)=3+\sqrt2\end{align}$$
Se Sun from City College Norwich in the UK, Junsu (David) from Bangkok Patana School in Thailand, Julian from British School Manila in the Philippines and Pablo from King's College Alicante in Spain used a slightly different very neat method, and Julian generalised further. This is Pablo's work:
Let $x$ be the top vertex, $y$ be the bottom left vertex and $z$ the remaining one
Therefore:
$$\begin{align}xy &= -6 + 2\sqrt2\\
xz &= 7 + 7\sqrt2\\
yz &= 2 - 4\sqrt2\end{align}$$
If we multiply them all together:
$$\begin{align}&(xy)(xz)(yz) = \left(-6 + 2\sqrt2\right)\left(7 + 7\sqrt2\right)\left(2 - 4\sqrt2\right)\\
\Rightarrow&x^2y^2z^2 = 2\left(-3 + \sqrt2\right)\times7\left(1 + \sqrt2\right)\times2\left(1 - 2\sqrt2\right)\\
\Rightarrow&(xyz)^2 = 28\times\left(-3 - 3\sqrt2 + \sqrt2 + 2\right)\left(1 - 2\sqrt2\right)\\
\Rightarrow&(xyz)^2 = 28\times\left(-1 - 2\sqrt2\right)\left(1 - 2\sqrt2\right)\\
\Rightarrow&(xyz)^2 = 28\times\left(-1 + 2\sqrt2 - 2\sqrt2 + 4\sqrt2\sqrt2\right)\\
\Rightarrow&(xyz)^2 = 28\times(-1+8)\\
\Rightarrow&(xyz)^2=196\\
\Rightarrow &xyz = \pm14\end{align}$$
Now we can replace the values of $xy$, $xz$ and $yz$ in that expression to find the values of the three variables, ie the vertices
Let $x = a + b\sqrt2$, $yz = 2 - 4\sqrt2$
$$\begin{align}\left(a + b\sqrt2\right)\left(2 - 4\sqrt2\right) &= \pm14\\
\Rightarrow2a - 4a\sqrt2 + 2b\sqrt2 - 8b &= \pm14\\
\Rightarrow (2a - 8b) + (-4a + 2b)\sqrt2 &= \pm14 + 0\sqrt2\end{align}$$
By comparison of coefficients:
Eq 1: $2a - 8b = \pm14$
Eq 2: $-4a + 2b = 0 \Rightarrow -2a + b = 0$
$$\begin{align}2a - 8b &= \pm14\\
+(-2a + b &= 0)\\
-7b& = \pm14
\Rightarrow b = ±2\end{align}$$
$$\begin{align}-2a + b &= 0\\
\Rightarrow2a &= b\\
\Rightarrow2a &= \pm2\\
\Rightarrow a &= \pm1\end{align}$$
So $x = 1 + 2\sqrt2$ or $-1 - 2\sqrt2$
Let $y = c + d\sqrt2$, $xz = 7 + 7\sqrt2$
$$\begin{align}\left(c + d\sqrt2\right)\left(7 + 7\sqrt2\right) &= ±14\\
\Rightarrow (c + 2d) + (c+d)\sqrt2 &= ±2 + 0\sqrt2\end{align}$$
By comparison of coefficients:
Eq 1: $c + 2d = ±2$
Eq 2: $c + d = 0$
Solving these equations gives:
$d = ±2$, $c = ∓2$ (in other words, whenever $d$ is +ve $c$ is -ve, and vice versa)
So $y = 2 - 2\sqrt2$ or $-2 + 2\sqrt2$
Let $z = e + f\sqrt2$, $xy = -6 + 2\sqrt2$
$$\begin{align}\left(e + f\sqrt2\right)\left(-6 + 2\sqrt2\right) &= ±14\\
\Rightarrow (-3e + 2f) + (e - 3f)\sqrt2 &= ±7 + 0\sqrt2\end{align}$$
By comparison of coefficients:
Eq 1: $-3e + 2f = ±7$
Eq 2: $e - 3f = 0$
Solving these equations gives:
$f = ±1$, $e = ±3$
So $z = 3 + \sqrt2$ or $-3 - \sqrt2$
Tommy from Costello Technology College in England used a very similar method, but that removed all division by surds:
Because the surd expressions are products, it is clear that multiplication/division is needed to solve the problem. There was nothing to divide by, so multiplying them together is the only option. The only relevant two are:
$$x^2yz = -28\sqrt2 - 14\\
x^2y^2z^2 = 196$$ Because the last one can be rephrased into $(xyz)^2$ and it is a square number, the square rooting gives the integer $14$, which is also $xyz$.
$\dfrac{x^2yz}{xyz}=x$, and as both of these variables are available, we can calculate the value of $x$. $$\frac{-28\sqrt2-14}{14}=-2\sqrt2-1=x$$
Tommy then divided $xy$ and $xz$ by $x$ by expressing them as surd fractions and rationalising the denominators, but this original method would also to find $y$ and $z$ without any division.
Amrit from Hymers College in the UK used a trick to remove the surds:
$$\begin{align} ab&=-6+2\sqrt2\\bc&=7+7\sqrt2\\ac&=2-4\sqrt2\end{align}$$ These equations can be written as $$\begin{align}\frac{ab+6}2&=\sqrt2\\\frac{bc-7}7&=\sqrt2\\\frac{2-ac}4&=\sqrt2\\\Rightarrow&\frac{ab+6}2=\frac{bc-7}7=\frac{2-ac}4\end{align}$$ Taking the left hand side of the three equations, $$7ab+42=2bc-14\Rightarrow b=\frac{56}{2c-7a}$$ This value of $b$ can be substitued into right hand side of the three equations above: $$\begin{align}&\frac{\tfrac{56c}{2c-7a}-7}7=\frac{2-ac}4\\
\Rightarrow&\frac{8c}{2c-7a}-1=\frac{2-ac}{4}\\
\Rightarrow&=\frac{6c+7a}{2c-7a}=\frac{2-ac}4\\
\Rightarrow&24c+28a=4c-2ac^2-14a+7a^2c\\
\Rightarrow&2ac^2-7a^2c+42a+20c=0\end{align}$$ Solving this quadratic for $c$ then multiplying both sides by $a$ $$ac=\frac{7a^2-20\pm\sqrt{49a^4-616a^2+400}}4$$ But we know that $ac=2-4\sqrt2$, therefore $$\begin{align}\frac{7a^2-20\pm\sqrt{49a^4-616a^2+400}}4&=2-4\sqrt2\\
\Rightarrow7a^2-20\pm\sqrt{49a^4-616a^2+400}&=8-16\sqrt2\\
\Rightarrow7a^2+16\sqrt2-28&=\pm\sqrt{49a^4-616a^2+400}\\
\Rightarrow\left(7a^2+\left(16\sqrt2-28\right)\right)^2&=49a^4-616a^2+400\\
\Rightarrow49a^2+14a^2\left(16\sqrt2-28\right)+\left(16\sqrt2-28\right)^2&=49a^4-616a^2+400\\
\Rightarrow\left(14\left(16\sqrt2-28\right)+616\right)a^2&=400-\left(16\sqrt2-28\right)^2\\
\Rightarrow 224\left(\sqrt2+1\right)a^2&=896\left(\sqrt2-1\right)\\
\Rightarrow a^2&=4\left(\sqrt2-1\right)^2\\
\Rightarrow a&=\pm\left(\sqrt2-1\right)\end{align}$$
And Amrit then found the values of $b$ and $c$ by substituting this back into the original equations.
Ed from Wyoming Valley West in the USA mostly used a trial method:
I first created a system of equations rigorously:
$$\begin{align}\left( a + b \sqrt{2} \right) \times \left(c + d \sqrt{2} \right) &= -6 + 2\sqrt{2}\\
\left(a + b\sqrt2\right) \times \left(e + f\sqrt2\right) &= 2 - 4\sqrt2\\
\left(c + d\sqrt2\right) \times \left(e + f\sqrt2\right) &=7 + 7\sqrt2\end{align}$$
To get a set of 6 equations for 6 unknown variables:
$$\begin{align}ac + 2bd &= -6\\
bc + ad & = 2\\
ae + 2bf &= 2\\
be + af &= -4\\
ce + 2df& = 7\\
de + cf &= 7\end{align}$$ My matrix background is shaky at best, so while I know creating a matrix would net a unique solution, I was certain I'd make a math error along the way, so I tried instead to deduce some things logically.
First I noted that from equation 5, both $c$ and $e$ must be odd.
Then, from equation 6, either $d$ is odd and $f$ is even, or vice versa.
Then I took a leap of faith that for all these sums to be bounded by $-6$ and $7$, all 6 values should be fairly small. And since equations 5 and 6 are both positive sums, all coefficients are likely positive as well.
From that, I tried a couple guesses, but then I hit paydirt with $c=1$, $d=2$, $e=3$, $f=1.$
Once I managed success from that combination, I tested it back into equations 1 & 2.
This yielded 2 equations with only 2 unknown variables, a much more manageable task.
Equation 1 became $a + 4b = -6$
and Equation 2 became $2a + b = 2$
resulting in $a = 2$ and $b = -2$.
I checked that result into equations 3 & 4, and everything checked on the math, but to make sure I didn't violate any rules of algebra, I checked the arithmagon and the math worked out nicely.
Jamie from BSB in the UK began by considering a simpler version of the problem to find a sensible method:

Next, set up a system of equations: $$\begin{align}xz&=132\hspace{20mm}&(1)\\xy&=11&(2)\\yx&=12&(3)\end{align}$$
from $(1)$ $z=\frac{132}x$ from $(2)$ $y=\frac{11}{x}$ from $(3)$ $y=\frac{12}z$
$\therefore \frac{11}x=\frac{12}z$
but $z=\frac{132}x$, so $\frac{11}x=\frac{12x}{132}$
and so $\frac{11\times132}{12}=x^2$
By repeating this process you can also find that $y^2=\frac{11\times12}{132}$ and $z^2=\frac{132\times12}{11}$
Jamie went on to apply this method to the problem:
From our previous research of multiplication arithmagons, we can deduce that $$\begin{align}b^2&=\frac{\left(7+7\sqrt2\right)\left(2-4\sqrt2\right)}{-6+2\sqrt2}\\
&=\frac{14-28\sqrt2+14\sqrt2-28\times2}{-6+2\sqrt2}\\
&=\frac{-14\left(3+\sqrt2\right)}{-2\left(3-\sqrt2\right)}\\
&=\frac{7\left(3+\sqrt2\right)\left(3+\sqrt2\right)}{\left(3-\sqrt2\right)\left(3+\sqrt2\right)}\\
&=\frac{7\left(9+6\sqrt2+2\right)}{9-2}\\
&=11+6\sqrt2\end{align}$$ $\left(11+6\sqrt2\right)$ can be expressed $\left(x+y\sqrt2\right)^2$ to allow for the square rooting of $b^2$. $$\begin{split} 11+6\sqrt2&=\left(x+y\sqrt2\right)^2\\&=x^2+2y^2+2xy\sqrt2\end{split}$$ Form simultaneous equations $$\begin{align}x^2+2y^2&=11\hspace{20mm}&(1)\\
2xy\sqrt2&=6\sqrt2&(2)\end{align}$$
From $(2)$, $2xy=6$ so $x=\frac3y$.
We can substitute this into $(1)$: $$\begin{align}x^2+2y^2&=11\\
\left(\frac3y\right)^2+2y^2&=11\\
\Rightarrow\frac{9+2y^4}{y^2}&=11\\
\Rightarrow2y^4-11y^2+9&=0\\
\Rightarrow(2y^2-9)(y^2-1)&=0\end{align}$$ Ignore $2y^2-1=0$ since $y$ should be an integer. If $y^2-1=0$ then $y=1$ or $y=-1$.
But $x=\frac3y$, so $x=3$ or $x=-3$ So $b=\pm\left(3+\sqrt2\right)$ $$\begin{align} ab&=7+7\sqrt2\\
\Rightarrow a&=\frac{7+7\sqrt2}{b}\\
\Rightarrow a&=\frac{7+7\sqrt2}{3+\sqrt2}\end{align}$$ Now, rationalise the denonimator $$\begin{align}a&=\frac{\left(7+7\sqrt2\right)\left(3-\sqrt2\right)}{\left(3+\sqrt2\right)\left(3-\sqrt2\right)}\\
\Rightarrow a&=\frac{21-7\sqrt2+21\sqrt2-14}7\\
\Rightarrow a&=\frac{7+14\sqrt2}7\\
\Rightarrow a&=1+2\sqrt2\end{align}$$ So $a=\pm\left(1+2\sqrt2\right)$
Now repeat for $c$.
Kryštof from The English College in Prague used the same method as Jamie, but without doing the 'research' first. This is Kryštof's work:
First we begin by assigning variables to the vertices of the triangle, $x$, $y$ and $z$ starting at the top and going clockwise.
Then we construct a system of three equations: $$\begin{align} xy&=7+7\sqrt{2}\hspace{20mm}&(1)\\
yz&=2-4\sqrt2&(2)\\
zx&=-6+2\sqrt2&(3)\end{align}$$ The method we will use is to make $y$ the subject of equation $(1)$ and $z$ the subject of equation $(3).$ Then we will substitute into equation $(2)$ to solve for $x$. $$\begin{align}y&=\frac{7+7\sqrt2}{x}\hspace{20mm}&(4)\\
z&=\frac{-6+2\sqrt2}{x}&(5)\end{align}\\$$
$$\begin{align}\frac{7+7\sqrt2}x.\frac{-6+2\sqrt2}x&=2-4\sqrt2\\
\Rightarrow\frac{\left(7+7 \sqrt {2}\right).(-6 +2 \sqrt {2})} {2-4 \sqrt {2}} &= x^2\end{align}$$ Kryštof then found $x$ using a calculator, but could have used Jamie's method shown above, or the method that Theodore uses below.
Theodore from Institut Saint-Lô in France and Mitali from Delhi Public School Sushant Lok in India both used a very neat method. This is Theodore's working.
We have:$$\begin{align} xy&=7+7\sqrt{2}\hspace{20mm}&(1)\\
yz&=2-4\sqrt2&(2)\\
zx&=-6+2\sqrt2&(3)\end{align}$$
$$\begin{align} \Rightarrow xy\times zx&=\left(7+7\sqrt2\right)\left(-6+2\sqrt2\right)\\
\Rightarrow x^2(yx)&=-42+14\sqrt2-42\sqrt2+28\\
&=-14-28\sqrt2\\
\Rightarrow x^2\left(2-4\sqrt2\right)&=-\left(14+28\sqrt2\right)\\
\Rightarrow x^2&=-\frac{14+28\sqrt2}{2-4\sqrt2}=-\frac{14\left(1+2\sqrt2\right)}{2\left(1-2\sqrt2\right)}\\
&=\frac{-7\left(1+2\sqrt2\right)^2}{1-8}=\left(1+2\sqrt2\right)^2\end{align}$$ Hence $x=1+2\sqrt2$
$$\begin{align}zx&=-6+2\sqrt2\\
\Rightarrow z&=\frac{-6+2\sqrt2}{1+2\sqrt2}=\frac{\left(-6+2\sqrt2\right)\left(1-2\sqrt2\right)}{1-8}\\
&=\tfrac{1}{-7}\left(-6+12\sqrt2+2\sqrt2-8\right)=\tfrac{1}{-7}\left(-14+14\sqrt2\right)=2-\sqrt2\end{align}$$
$$\begin{align}xy&=7+7\sqrt2\\
\Rightarrow y=&\frac{7+7\sqrt2}{1+2\sqrt2}=\frac{\left(7+7\sqrt2\right)\left(1-2\sqrt2\right)}{1-8}\\
&=-\tfrac17\left(7-14\sqrt2+7\sqrt2-28\right)=-\tfrac17\left(-21-7\sqrt2\right)=3+\sqrt2\end{align}$$
Se Sun from City College Norwich in the UK, Junsu (David) from Bangkok Patana School in Thailand, Julian from British School Manila in the Philippines and Pablo from King's College Alicante in Spain used a slightly different very neat method, and Julian generalised further. This is Pablo's work:
Let $x$ be the top vertex, $y$ be the bottom left vertex and $z$ the remaining one
Therefore:
$$\begin{align}xy &= -6 + 2\sqrt2\\
xz &= 7 + 7\sqrt2\\
yz &= 2 - 4\sqrt2\end{align}$$
If we multiply them all together:
$$\begin{align}&(xy)(xz)(yz) = \left(-6 + 2\sqrt2\right)\left(7 + 7\sqrt2\right)\left(2 - 4\sqrt2\right)\\
\Rightarrow&x^2y^2z^2 = 2\left(-3 + \sqrt2\right)\times7\left(1 + \sqrt2\right)\times2\left(1 - 2\sqrt2\right)\\
\Rightarrow&(xyz)^2 = 28\times\left(-3 - 3\sqrt2 + \sqrt2 + 2\right)\left(1 - 2\sqrt2\right)\\
\Rightarrow&(xyz)^2 = 28\times\left(-1 - 2\sqrt2\right)\left(1 - 2\sqrt2\right)\\
\Rightarrow&(xyz)^2 = 28\times\left(-1 + 2\sqrt2 - 2\sqrt2 + 4\sqrt2\sqrt2\right)\\
\Rightarrow&(xyz)^2 = 28\times(-1+8)\\
\Rightarrow&(xyz)^2=196\\
\Rightarrow &xyz = \pm14\end{align}$$
Now we can replace the values of $xy$, $xz$ and $yz$ in that expression to find the values of the three variables, ie the vertices
Let $x = a + b\sqrt2$, $yz = 2 - 4\sqrt2$
$$\begin{align}\left(a + b\sqrt2\right)\left(2 - 4\sqrt2\right) &= \pm14\\
\Rightarrow2a - 4a\sqrt2 + 2b\sqrt2 - 8b &= \pm14\\
\Rightarrow (2a - 8b) + (-4a + 2b)\sqrt2 &= \pm14 + 0\sqrt2\end{align}$$
By comparison of coefficients:
Eq 1: $2a - 8b = \pm14$
Eq 2: $-4a + 2b = 0 \Rightarrow -2a + b = 0$
$$\begin{align}2a - 8b &= \pm14\\
+(-2a + b &= 0)\\
-7b& = \pm14
\Rightarrow b = ±2\end{align}$$
$$\begin{align}-2a + b &= 0\\
\Rightarrow2a &= b\\
\Rightarrow2a &= \pm2\\
\Rightarrow a &= \pm1\end{align}$$
So $x = 1 + 2\sqrt2$ or $-1 - 2\sqrt2$
Let $y = c + d\sqrt2$, $xz = 7 + 7\sqrt2$
$$\begin{align}\left(c + d\sqrt2\right)\left(7 + 7\sqrt2\right) &= ±14\\
\Rightarrow (c + 2d) + (c+d)\sqrt2 &= ±2 + 0\sqrt2\end{align}$$
By comparison of coefficients:
Eq 1: $c + 2d = ±2$
Eq 2: $c + d = 0$
Solving these equations gives:
$d = ±2$, $c = ∓2$ (in other words, whenever $d$ is +ve $c$ is -ve, and vice versa)
So $y = 2 - 2\sqrt2$ or $-2 + 2\sqrt2$
Let $z = e + f\sqrt2$, $xy = -6 + 2\sqrt2$
$$\begin{align}\left(e + f\sqrt2\right)\left(-6 + 2\sqrt2\right) &= ±14\\
\Rightarrow (-3e + 2f) + (e - 3f)\sqrt2 &= ±7 + 0\sqrt2\end{align}$$
By comparison of coefficients:
Eq 1: $-3e + 2f = ±7$
Eq 2: $e - 3f = 0$
Solving these equations gives:
$f = ±1$, $e = ±3$
So $z = 3 + \sqrt2$ or $-3 - \sqrt2$
Tommy from Costello Technology College in England used a very similar method, but that removed all division by surds:
Because the surd expressions are products, it is clear that multiplication/division is needed to solve the problem. There was nothing to divide by, so multiplying them together is the only option. The only relevant two are:
$$x^2yz = -28\sqrt2 - 14\\
x^2y^2z^2 = 196$$ Because the last one can be rephrased into $(xyz)^2$ and it is a square number, the square rooting gives the integer $14$, which is also $xyz$.
$\dfrac{x^2yz}{xyz}=x$, and as both of these variables are available, we can calculate the value of $x$. $$\frac{-28\sqrt2-14}{14}=-2\sqrt2-1=x$$
Tommy then divided $xy$ and $xz$ by $x$ by expressing them as surd fractions and rationalising the denominators, but this original method would also to find $y$ and $z$ without any division.
Amrit from Hymers College in the UK used a trick to remove the surds:
$$\begin{align} ab&=-6+2\sqrt2\\bc&=7+7\sqrt2\\ac&=2-4\sqrt2\end{align}$$ These equations can be written as $$\begin{align}\frac{ab+6}2&=\sqrt2\\\frac{bc-7}7&=\sqrt2\\\frac{2-ac}4&=\sqrt2\\\Rightarrow&\frac{ab+6}2=\frac{bc-7}7=\frac{2-ac}4\end{align}$$ Taking the left hand side of the three equations, $$7ab+42=2bc-14\Rightarrow b=\frac{56}{2c-7a}$$ This value of $b$ can be substitued into right hand side of the three equations above: $$\begin{align}&\frac{\tfrac{56c}{2c-7a}-7}7=\frac{2-ac}4\\
\Rightarrow&\frac{8c}{2c-7a}-1=\frac{2-ac}{4}\\
\Rightarrow&=\frac{6c+7a}{2c-7a}=\frac{2-ac}4\\
\Rightarrow&24c+28a=4c-2ac^2-14a+7a^2c\\
\Rightarrow&2ac^2-7a^2c+42a+20c=0\end{align}$$ Solving this quadratic for $c$ then multiplying both sides by $a$ $$ac=\frac{7a^2-20\pm\sqrt{49a^4-616a^2+400}}4$$ But we know that $ac=2-4\sqrt2$, therefore $$\begin{align}\frac{7a^2-20\pm\sqrt{49a^4-616a^2+400}}4&=2-4\sqrt2\\
\Rightarrow7a^2-20\pm\sqrt{49a^4-616a^2+400}&=8-16\sqrt2\\
\Rightarrow7a^2+16\sqrt2-28&=\pm\sqrt{49a^4-616a^2+400}\\
\Rightarrow\left(7a^2+\left(16\sqrt2-28\right)\right)^2&=49a^4-616a^2+400\\
\Rightarrow49a^2+14a^2\left(16\sqrt2-28\right)+\left(16\sqrt2-28\right)^2&=49a^4-616a^2+400\\
\Rightarrow\left(14\left(16\sqrt2-28\right)+616\right)a^2&=400-\left(16\sqrt2-28\right)^2\\
\Rightarrow 224\left(\sqrt2+1\right)a^2&=896\left(\sqrt2-1\right)\\
\Rightarrow a^2&=4\left(\sqrt2-1\right)^2\\
\Rightarrow a&=\pm\left(\sqrt2-1\right)\end{align}$$
And Amrit then found the values of $b$ and $c$ by substituting this back into the original equations.