Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Folding Squares
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Talei from Poltair Community School and Sports College sent in this excellent solution to the problem, showing the diagonals are split in the ratio 1:2 (or equivalently that the smaller part is a third of the whole)
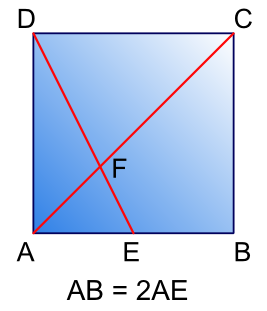
FD = 2EF and FC = 2AF because . . .
We can prove that triangle FCD is an enlargement, by a scale factor of 2, of the triangle AEF.
The triangles' angles are the same - at point F the crossing lines give each triangle an identical angle because they are opposite each other. The line AC joins parallel lines to give an identical angle to each triangle because they are alternate, and the line ED works in the same way.
Therefore, because AE must be exactly half the length of CD, each line in triangle AEF will be half of its enlarged equivalent in triangle FCD.
FD = 2EF because FD is the enlarged equivalent line of EF in triangle AEF.
FC = 2AF because FC is the enlarged equivalent line of AF in triangle AEF.
Talei's method using similar triangles can also be applied to the general case for a pallelogram and arbitary intersection point:
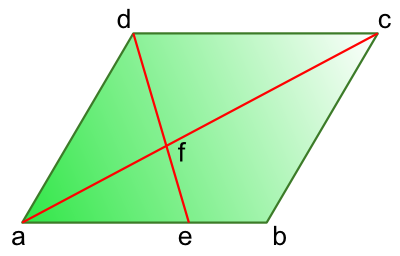
$$\mathrm{\angle afe = \angle cfd \textrm{ (opposite angles) and } \angle eaf = \angle dcf \textrm{ (alternate / 'Z-' angles)}}$$
$$\mathrm{\therefore \triangle aef \textrm{ is similar to }\triangle cdf \Rightarrow \frac{cf}{af} = \frac{cd}{ae} \Rightarrow cf = \frac{cd}{ae}af}$$
$$\mathrm{ac = af + cf \Rightarrow ac = af \left( 1 + \frac{cd}{ae} \right)}$$
$$\mathrm{\therefore \ af = \frac{1}{1 + \frac{cd}{ae}} \textrm{ multiplying through by ae and using cd = ab} \Rightarrow af = \frac{ae}{ae + ab} ac}$$
You may also like
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Pareq Exists
Prove that, given any three parallel lines, an equilateral triangle always exists with one vertex on each of the three lines.
The Medieval Octagon
Medieval stonemasons used a method to construct octagons using ruler and compasses... Is the octagon regular? Proof please.