Copyright © University of Cambridge. All rights reserved.

'Folding Squares' printed from https://nrich.maths.org/

Show menu

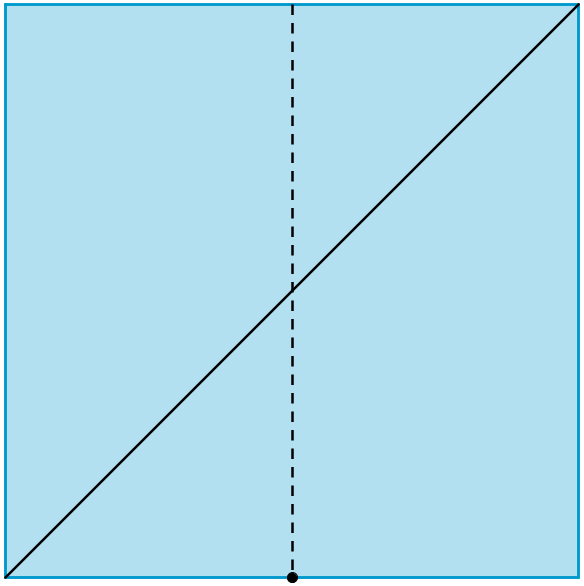
Start with a square...

Fold to create a diagonal running from bottom left to top right.	Find the midpoint of the base by folding.	Fold the paper again, joining the top left corner to the midpoint of the base.	What fractions of the diagonal do you think your new fold has created?

Measure the two sections of the diagonal and compare their lengths.

What do you notice?
Is this what you expected?

 

Can you produce a convincing mathematical argument or proof that justifies what you have found?

You might like to try A Parallelogram Trisection and Folding Fractions next.