Copyright © University of Cambridge. All rights reserved.
'Funny Factorisation' printed from https://nrich.maths.org/
Show menu
Funny Factorisation printable worksheet
Some 4 digit numbers can be written as the product of a 3 digit number and a 2 digit number using each of the digits $1$ to $9$ once, and only once.
The number $4396$ can be written as just such a product.
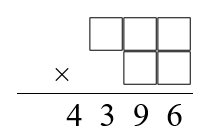
Can you find the factors?
Maths is full of surprises!
The numbers $5796$ and $5346$ can each be written as a product like this in two different ways.
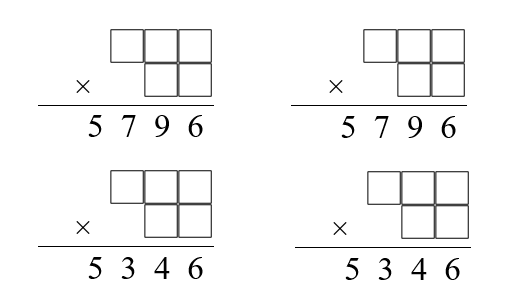
Can you find these four funny factorisations?
Extension
There are two more funny factorisations to find, using each of the digits $1$ to $9$ once, and only once.
Can you fill in the blanks in the multiplication below to find one of them?
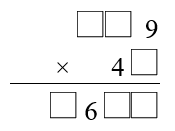
If you know a bit about computer programming, you may wish to write a program to find the final funny factorisation.