It must be 2000
Problem
We're going to have a look at this number - $2000$.
We've used all sorts of numbers in the past, so let's use our detective skills to find things out about this number $2000$.
It looks like $2000$ because we count in tens and along in a straight line:-
Sometimes, yes some "TIMES" we count in a circle.
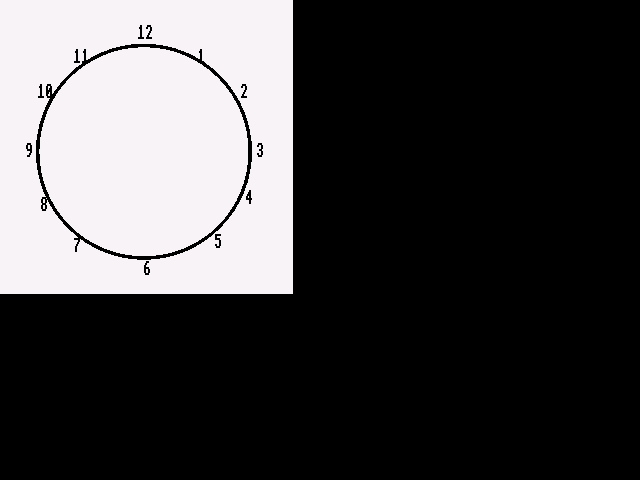
If we started counting around this "$12$" clock and counted up to $2000$ we would end up at the number $8$.
But of course we could count in a circle of any size with a different number of numbers around it.
So if the "clock" looked like this:
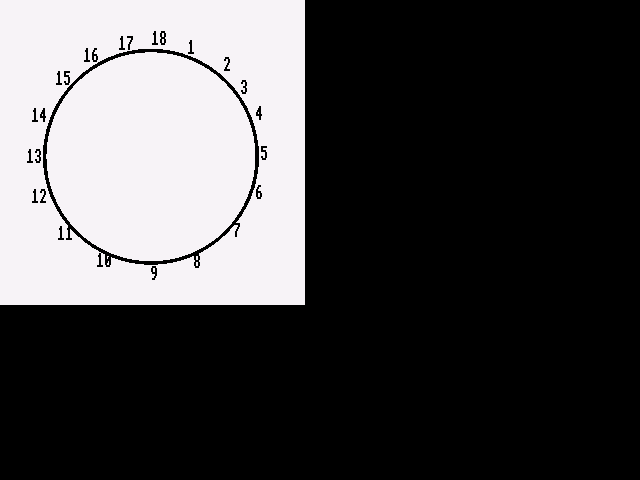
and we counted up to $18$ before returning to $1$, then we would end up at $2$ if we counted to $2000$.
Some of you will know about this kind of counting already, it is sometimes called MODULO arithmetic or CLOCK arithmetic.
Thinking about it is all to do with remainders. Like this:
$2000$ divided by $12$ will be $166$ remainder $8$
$2000$ divided by $18$ will be $111$ remainder $2$
So we could just look at remainders.
Well save your brains!! I used a spreadsheet on my computer and got the following table.
Column A is the number of numbers around the clock, or the modulo number.
Column B is the remainder when divided into $2000$!
And just for fun I added column A to column B to get column C.
Just explore and explore ... Be a detective ... Look, think ... write what you notice and what you think.
Some of you may have also thought about working in different bases. We usually work in base ten, and you may have explored base $2$.
If you are counting $2000$ dots then the number looks like this :-
| Base | Number |
| $2$ | $110110000$ |
| $3$ | $2202002$ |
| $4$ | $133100$ |
| $5$ | $31000$ |
| $6$ | $13133$ |
| $7$ | $5555$ |
| $8$ | $3720$ |
| $9$ | $2662$ |
| and | |
| $10$ | $20004 |
Well, what an interesting collection of $3$s and $1$s in bases $4$, $5$ and $6$. I found base $7$ to be a very big surprise.
I have not looked deeply into this, I thought I'd leave it up to you.
We're always asking "I wonder what would happen if I ...?"
So what if the triangles were made differently?
Like this one:-
Then, for my final contribution, and eagerly waiting to receive your contributions, I offer you this splendid picture:-
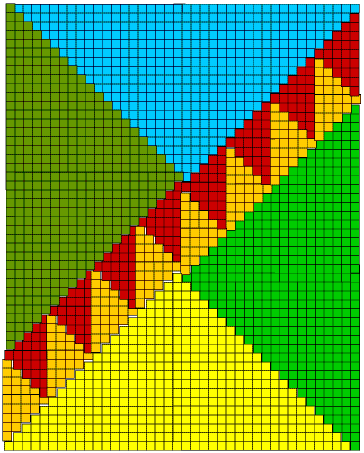
This has four large triangles, the $20$th in their sequence each with an area of $400$.
There are $16$ small triangles, the $5$th in their sequence each with an area of $25$.
So you see the total area is $2000$!
Student Solutions
There are lots of answers to this problem, depending on what questions you choose to ask.
Have a go yourself, and if you discover anything interesting, e-mail us to tell us what you've done! Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried. Teachers - you might like to send in a summary of your children's work.