 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
More Dicey Decisions



- Problem
- Student Solutions
- Teachers' Resources
Here's an example of a net for a dodecahedral die with the opposite numbers summing to 13:
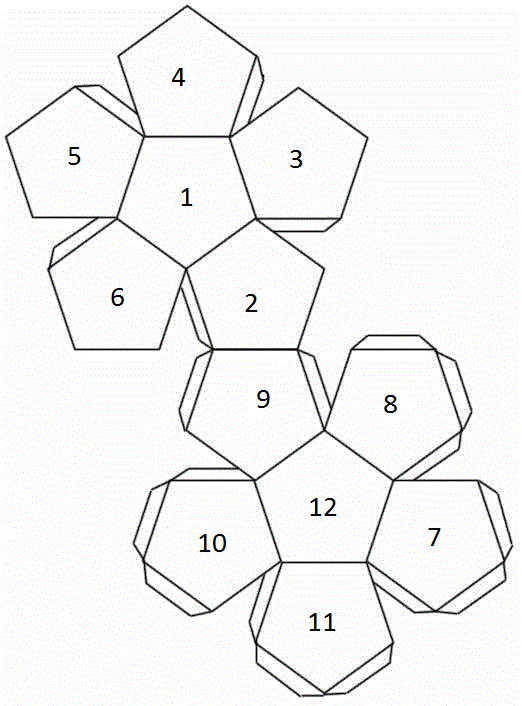
For such a dodecahedral die with the numbers 2,3,4,5,6 around 1, and opposite faces summing to 13, the edge totals are:
| Edge 1 | Edge 2 | Sum | Edge 1 | Edge 2 | Sum | |
| 1 | 2 | 3 | 1 | 3 | 4 | |
| 1 | 4 | 5 | 1 | 5 | 6 | |
| 1 | 6 | 7 | 2 | 3 |
5 |
|
| 2 | 6 | 8 | 2 | 9 | 11 | |
| 2 | 8 | 10 | 3 | 4 | 7 | |
| 3 | 4 | 7 | 3 | 8 | 11 | |
| 3 | 7 | 10 | 4 | 5 | 9 | |
| 4 | 7 | 11 | 4 | 11 | 15 | |
| 5 | 6 | 11 | 5 | 11 | 16 | |
| 5 | 10 | 15 | 6 | 10 | 16 | |
| 6 | 9 | 15 | 9 | 8 | 17 | |
| 9 | 10 | 19 | 9 | 12 | 21 | |
| 8 | 7 | 15 | 8 | 12 | 20 | |
| 7 | 11 | 18 | 7 | 12 | 19 | |
| 11 | 10 | 21 | 11 | 12 | 23 |
If we plot the frequency distribution for the possible scores for this die we get:
| Score | Frequency | Score | Frequency | |
| 3 | 1 | 13 | 0 | |
| 4 | 1 | 14 | 0 | |
| 5 | 2 | 15 | 4 | |
| 6 | 1 | 16 | 2 | |
| 7 | 2 | 17 | 1 | |
| 8 | 1 | 18 | 1 | |
| 9 | 1 | 19 | 2 | |
| 10 | 2 | 20 | 1 | |
| 11 | 4 | 21 | 2 | |
| 12 | 0 | 22 | 1 | |
| 23 | 1 |
This is a symmetric distribution with a mean score of 13. It turns out all possible dodecahedral dice with faces summing to 13 have this property. Consider swapping two of the faces, say 2 and 3, which will also swap 11 and 10 on the opposite side of the die. The sum of the edge between 2 and 3, and 11 and 10 will stay the same, however the other edges of these faces will either increase or decrease by 1. The edge between faces A and B, say, will change in the opposite direction to the edge between the faces (13-A) and (13-B), as if A, say, increases by 1, (13-A) will decrease by 1. It follows from this that the distribution of the row sums will remain symmetric.
In general, you can prove that swapping two arbitrary faces can be done as the product of swapping pairs of adjacent faces, and as we've just shown the simpler process of just swapping one pair of faces leaves the distribution symmetric, we've therefore shown that all swaps will.
For our example, we have the corner sums:
| Faces | Sum | Faces | Sum | Faces | Sum | Faces | Sum | |||
| 1,2,3 | 6 | 2,3,8 | 13 | 4,5,11 | 20 | 7,8,12 | 27 | |||
| 1,3,4 | 8 | 2,6,9 | 17 | 4,7,11 | 22 | 7,11,12 | 30 | |||
| 1,4,5 | 10 | 2,8,9 | 19 | 5,6,10 | 21 | 8,9,12 | 29 | |||
| 1,2,6 | 9 | 3,4,7 | 14 | 5,10,11 | 26 | 9,10,12 | 31 | |||
| 1,5,6 | 12 | 3,7,8 | 18 | 6,9,10 | 25 | 10,11,12 | 33 |
These have an average of 19.5, and are also symmetrically distributed about that point. The same argument given for the edges remaining symmetric under the exchange of faces can be adapted to prove the claim that the corner sums remain symmetrically distributed when pairs of faces are swapped.
The important fact throughout these arguments is that the opposite faces always add up to 13. If this wasn't the case, then the distribution would not remain symmetric under the swapping of all pairs of faces.