Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Beelines
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
No one sent us a complete solution to this problem, but here is the start of a solution which shows some good mathematical thinking and a systematic way of working.
We decided to investigate what happens if you keep the $x$ coordinate the same and change the $y$ coordinate. Here is our table to show the number of squares and gridlines crossed when the $x$ coordinate is $5$.
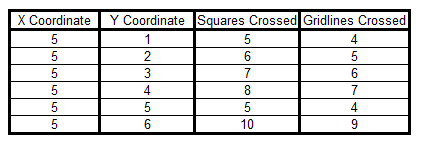
We noticed a pattern for the number of squares crossed, which works for every $y$ coordinate we tried except $5$. If you add together the $x$ and $y$ coordinates and take away 1, you get the number of squares crossed. This is because for example to get from (0,0) to (5,3) you go along 5 squares and up 3 squares, meaning that you travel through 8 squares altogether, but that counts the corner square twice so you need to take away 1.
It doesn't work for (5,5) because you go diagonally through the corners of the squares instead of cutting through the edges.
Can anybody build on this thinking and explain the patterns found?
Update: Jacky from Merici College in Canberra, Australia, drew some diagrams and compiled tables to try to notice some patterns.
Alex (also from Merici College) sent us the following solution that offers a formula. Does it always work?
I have found through investigation that we can predict the number of squares a line passes through starting at 0 using the formula:
(A) Number of squares = ( x + y ) - (highest common factor of x and y)
This is why:
In my investigation I found the common pattern of:
(B) Number of squares = (x + y ) - 1 worked for some of the coordinates. I then tried to spot a pattern within these numbers and found that it occurred if either x or y was a prime number. Using this fact I investigated further and found that a common relationship with all the numbers was x and y's highest common factor.
After I figured this out, I could see that the absolute highest amount of squares a line could go through used the formula B.
Here's an example: Imagine line goes from (0,0) to (4,12). The highest common multiple of (4,12) is 4. This line goes through the intersection point of squares at point (1,4), (2,8) and (3,12).
Because this line goes through these intersections instead of crossing squares, 3 squares are 'missed', plus the original 1 in the formula B, which reduces the number of squares by 4.
Well done, Alex and Jacky!
You may also like
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Nim
Start with any number of counters in any number of piles. 2 players take it in turns to remove any number of counters from a single pile. The loser is the player who takes the last counter.
Loopy
Investigate sequences given by $a_n = \frac{1+a_{n-1}}{a_{n-2}}$ for different choices of the first two terms. Make a conjecture about the behaviour of these sequences. Can you prove your conjecture?