Steve writes

 

Once I had understood the scoring systems I realised that I needed to look at the chances of winning based on whether I reached deuce or not. Let $V$ be the event of victory in the the overall game and $D$ the event of reaching deuce ($3$ points all) and $P_0, P_1$ and$P_2$ the probability of winning the game whilst losing $0$, $1$ and $2$ points respectively.

 

$$P(V) = P_0+P_1+P_2+ P(V|D)P(D)$$

$P_0, P_1$ and$P_2$ correspond to games of $4$, $5$ and $6$ points respectively. Each of these must end in a winning point (denoted W). The number of such games equals the number of ways of distributing $0$, $1$ and $2$ lost points (denoted L) amongst $3$, $4$ and $5$ points. The game reaches deuce if $6$ points are played with $3$ $W$s and $3$ $L$s. The number of such games equals the number of ways of distributing $3$ $L$s into $6$ points. Since each point is won or lost independently of the other points the probabilities multiply. Therefore,

$$P(V) = (0.6)^4\cdot 1 + (0.6)^4(0.4)\cdot 4 + (0.6)^4(0.4)^2\cdot \frac{5\cdot 4}{2}+P(V|D)\cdot(0.6)^3(0.4)^3\cdot\frac{6\cdot 5\cdot 4}{3\cdot 2}$$

I now need to use conditional probability to work out the chance of winning given that I reach deuce

The red dots on this tree indicate branches where the probability of winning equals the probability of winning given that I am at deuce $P(V|D)$ and the blue dot is a victory $V$.

$$P(V|D) = (0.6)^2 + (0.6)(0.4)P(V|D)+(0.4)(0.6)P(V|D)$$

which can be rearranged to

$$P(V|D) = \frac{(0.6)^2}{1-2(0.6)(0.4)}$$

Putting all of this together yields a probability of victory of

$$P(V) =(0.6)^4\left[ 1+ 4(0.4)+10(0.4)^2\right] +\frac{20(0.6)^5(0.4)^3}{1-2(0.6)(0.4)}$$

This equals $0.736$ (3dp). I left the probabilities in so that I could check the calculation by replacing the $0.6$ and $0.4$ by $0.5$. In this case, I get $0.5$, which makes sense (even players have an even chance of winning in this set of game rules). I also get a guaranteed victory by changing the $0.6$ to $1$ and setting the $0.4$ to $0$, which also makes sense (you will win if you win every point!)

 

 

--------------

 

For the second part of the problem I used a spreadsheet. It was inefficient, but displayed the probabilities clearly. After a bit of thought it is clear that the $P(V|D)$ depends on whether deuce was reached on a $W$ or on a $L$. I'll need two new events $D_W$ and $D_L$ for these cases.

We now have

$$P(V)= P(V|\bar{D})P(\bar{D})+P(V|D_L)P(D_L)+P(V|D_W)P(D_W)$$

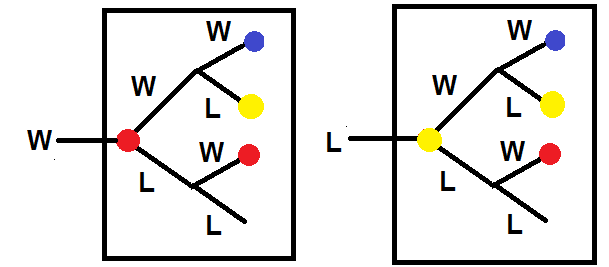
There is a fun pair of linked trees for the $P(V|D)$ - in the diagram the red circles represent $P(V|D_W)$ and the yellow circles represent $P(V|D_L)$. Reading off the probabilities gives a pair of simultaneous equations:

 

$$P(V|D_W) = (0.8)^2+(0.8)(0.2)P(V|D_L)+(0.2)(0.4)P(V|D_W)$$

$$P(V|D_L)=(0.4)(0.8)+(0.4)(0.2)P(V|D_L)+(0.6)(0.4)P(V|D_W)$$

This gives $P(V|D_W) = 0.792$ (exact value $\frac{80}{101}$) and $P(V|D_L) = 0.554$ (exact value $\frac{56}{101}$)

 

Using this piece of conditional probability to simplify the numerical analysis I then used a spreadsheet (Tennis.xls ) to calculate that

$$P(D_L) = 0.0755, \quad P(D_W) = 0.0947$$

Using this I calculate the chance of victory as

$$P(V) = 0.7364$$

 

For Bryony the numbers are

$$\begin{eqnarray}P(V|D_W) = 0.753\\P_(V|D_L)=  0.423\\P(D_L) = 0.0857\\P(D_W)= 0.0646\\P(V) =0.7383\end{eqnarray}$$

So, the players are very evenly matched.

 

You can check the results on this spreadsheet: Tennis.xls