Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Which Is Bigger?
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
$n+10$ and $2n+3$
Luca from St François High School - Troyes in France, Son Charles from Rock High School, Tororo in Uganda and Maria from Colston's Girls' School in the UK all tested different values. This is Maria's work:
Anh Minh from British Vietnamese International School Hanoi in Vietnam, Ben from Pembury in the UK, Leo from Kings Al Barsha in UAE, Kevin from West Island School in Hong Kong, Justin from Dulwich College Seoul in South Korea, Jonathan from Ashmole Academy in the UK, Ana from UAE, Luca and Maria showed this on a graph. This is Luca's work, using GeoGebra:
Let's create two different functions :
$f(n) = n +10$ ; and $g(n) = 2n +3$, corresponding to the expressions given in the exercise.
Thanks to Geogebra, we can then create the functions' representative curves.
We obtain the following curves
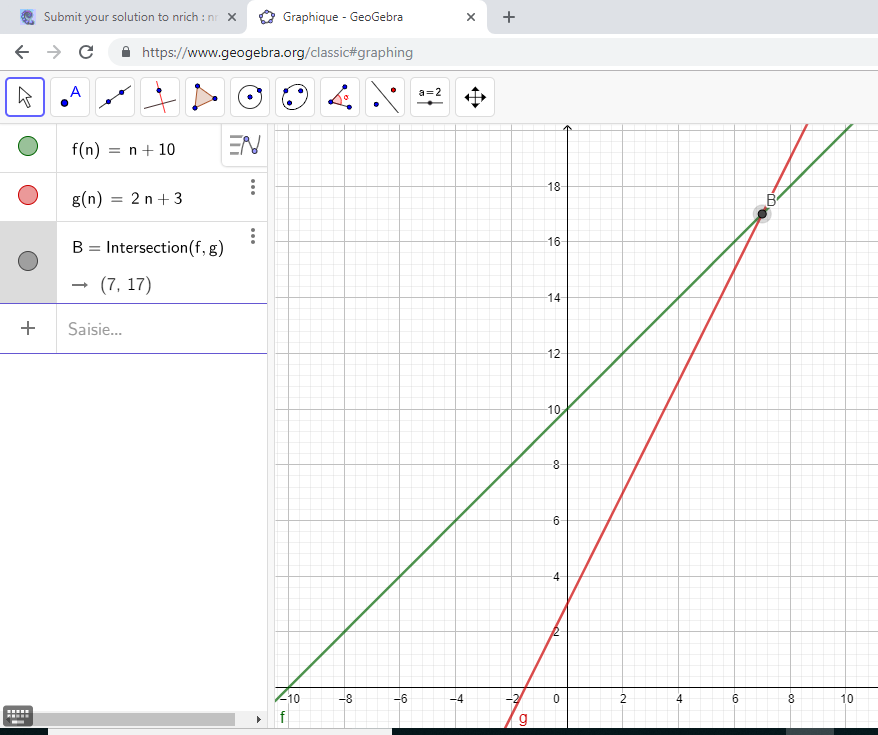
On the picture, the two curves cut [intersect] at B. Its [coordinates] are (7 , 17). This corresponds to what we found in the table.
Clara from Herlufsholm in Denmark, Archisman from the Future Foundation School in India and Ron, Ata, Jonathan and Mitra from Ashmole Academy sent in this answer:
If you substitute $n$ with something smaller than $7$, $n+10$ is smaller.
If you substitute $n$ with $7$, then both $n+10$ and $2n+3$ are equal.
If you substitute $n$ with something bigger than $7$, $2n+3$ is bigger.
Leo explained why one expression grows faster than the other:
This scenario was created because $n+10$ goes up by $1$ every time you increase the value of $n.$ However $2n+3$ goes up by $2$ every time you increase the value of $n$ (by one).
Clara explained why the two expressions behave differently for different values of $n$:
This is because $2n+3$ is multiplying the number by $2$ and not adding that very much on to the number. With small numbers such as $1$ and $2$ multiplying the number has very little effect compared to adding $10$ to the number.
However, with bigger numbers such as $37426$, by doubling it the number has significantly increased compared to if $10$ was added to the number.
Naomi and Justin from Dulwich College Seoul showed how this leads to a cut-off of 7. This is Naomi's work:
If you want $2n+3$ to be bigger than $n+10,$ then your $n+3$ has to be bigger than $10.$ Which means if your $n$ is bigger than $7$, $2n+3$ will be bigger than $n+10$
Adithya from Hymers College in the UK, Yoochan from Dulwich College Seoul and Ana wrote this algebraically. This is Yoochan's work:
Let's first say that $n+10$ is greater than $2n+3.$ Then the equation [inequality] goes:
$n+10 \gt 2n+3$
then, subtract $n$ from each side:
$10 \gt n+3$
subtract $3$ from each side:
$7 \gt n$
This shows that if $n$ is smaller than $7$, $n+10$ is greater than $2n+3$.
Now, let's look at if $2n+3$ is greater than $n+10.$ Then the equation [inequality] will go:
$2n+3 \gt n+10$
like the previous equation, subtract $n$ from each side:
$n+3 \gt 10$
and subtract $3$:
$n \gt 7$
So, this shows that if n is greater than $7$, $2n+3$ is greater than $n+10$.
$2n+7$ and $4n+11$
Clara said that $4n+11$ is bigger.
Ana created this graph:
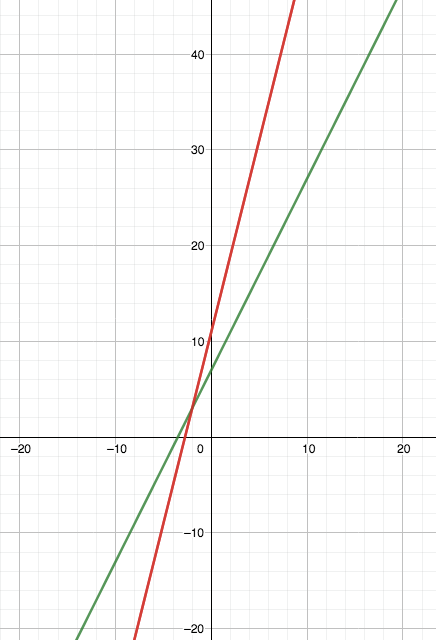
The red line is $y=4x+11$ and the green line is $y=2x+7$
On a graph we can see that the point of intersection is $(-2, 3)$
So when $n\gt -2$ then $4n+11\gt 2n+7$ and when $n\lt -2$ then $4n+11\lt 2n+7$
Yoochan, Justin and Adithya used algebra. This is Adithya's work:
$\begin{align} 2n+7&\gt 4n + 11\\
-2n&\gt 4\\
n&\lt-2\end{align}$
$\begin{align} 4n+11&\gt 2n+7\\
2n&\gt -4\\
n&\gt-2\end{align}$
Using the two inequalities above we can establish that for values where $n\lt-2,$ the expression $2n+7$ is greater and for values where $n\gt-2,$ the expression $4n+11$ is bigger.
$2(3n+4)$ and $3(2n+4)$
Ana used a graphical solution:
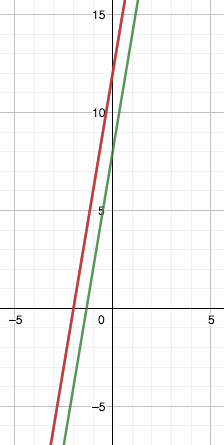
The green line is $y=2(3n+4)$ and the red line is $y=3(2n+4).$
As can be seen on the graph, they are parallel lines because they have the same gradient but different constants. As a result of them being parallel lines, one of them must always be bigger. In this case we can see it is the red line, $3(2n+4).$
Further, if the expressions are rearranged they become $6n+8$ and $6n+12.$ This makes it more obvious that the second expression will always be bigger.
Yoochan, Justin and Adithya also used algebra. This is Yoochan's work:
Let's first simplify $2(3n+4)$ and $3(2n+4)$ to $6n+8$ and $6n+12$
If $6n+8$ is greater than $6n+12$:
$6n+8 \gt 6n+12$
Divide by $2$:
$3n+4 \gt 3n+6$
Subtract $3n$:
$4 \gt 6$
If $6n+8$ is greater than $6n+12$, we get an equation of $4$ is greater than $6$, which is totally wrong. So, this proves that $6n+8$ cannot be greater than $6n+12$, and $6n+12$ is always greater than $6n+8$, so matter what the value of $n$ is.
$2(3n+3)$ and $3(2n+2)$
Clara and Ben said that the expressions are the same. Ben explained why:
I found that with the expressions $3(2n+2)$ and $2(3n+3)$ they always total an equal amount due to the sole fact that you add the number which you multiplied $n$ by. These two numbers are $2$ and $3$. If you've added $2$ you times by $3$ and if you add $3$ you times by $2$ this then leads to an equal amount.
Adithya, Ana, Justin and Yoochan used algebra. This is Yoochan's work:
$2(3n+3)$ and $3(2n+2)$
Let's simplify this to $6n+6$ and $6n+6.$
We can see that these two are equal in value, so no matter what $n$ will be, these two equations have the same output.
Find two expressions so that one is bigger whenever $n\lt5$ and the other is bigger whenever $n\gt5.$
Clara: $2n$ and $n+5$
Nathan from British Vietnamese International School: $n+9$ and $2n+4$
Nathan showed this works by substituting different values of $n$.
Adithya explained some reasoning which helps to find the expressions:
To find two expressions that satisfy the above constraints, the two expressions must be equal to each other when $n$ takes a value of $5$.
For example, $n+7$ and $2n+2$ would be two feasible expressions.
Siddhant from Singapore International School used this fact:
I took a positive coefficient of $x$ and added it to a constant, to give a larger coefficient of $x.$ This gives us the equation:
$2x + n = 3x$
Now I substituted $x$ to be $5$, as only then would the two [expressions] be equal to each other.
$2(5) + n = 3(5)\\
10 + n = 15\\
n = 5$
Therefore, the two expressions are:
$2x + 5$ and $3x$
I then plotted this on a graph, and inferred that when $x\lt5$, the line $2x+5$ is greater than $3x.$ When $x\gt5$, the line $3x$ is greater than $2x+5$
Ana also constructed two expressions which are equal when $n=5$:
The point of intersection of the expressions must be $x=5$. $$\begin{align}x&=5\\
3x&=2x+5\\
18x&=12x+30\end{align}$$
I added $2x$ then multiplied both expressions by $6$ to reach two expressions with an intersection point of $5.$ So when $n\gt 5$ then $18n\gt 12n+30$ and when $n\lt 5$ then $18n\lt 12n+30.$
Justin started from an inequality and 'solved' it backwards: $$\begin{align} n&\lt5\\
2n&\lt n+5\\
2n+3&\lt n+8\end{align}$$
$n+8$ is bigger whenever $n\lt5$, and $2n+3$ is bigger whenever $n\gt5.$
Find three expressions so that the first is biggest whenever $n\lt0$, the second is biggest whenever $n$ is between $0$ and $4$, and the third is biggest whenever $n\gt4.$
Clara and Nathan substituted in whole numbers to check that their inequalities worked.
Nathan: $10-n$, $n+\frac{17}2$ and $2n+4$
Clara: $-n$, $n+5$ and $2.1n$
I tried to keep the numbers simple as there is no need to overcomplicate things. However I got the $2.1$ because $2$ worked but eventually there would be two numbers that where the same so $2.1$ was the easiest option to change to. I used excel to help me with this as it did all the sums for me really quickly and it was easy to make small iterations.
I multiplied $n$ by a negative a lot because it meant that as $n$ increased, $-n$ decreased making it easy to use when one formula had to be bigger than the other at only a certain point.
Siddhant and Ana used graphs again. This is Ana's work:
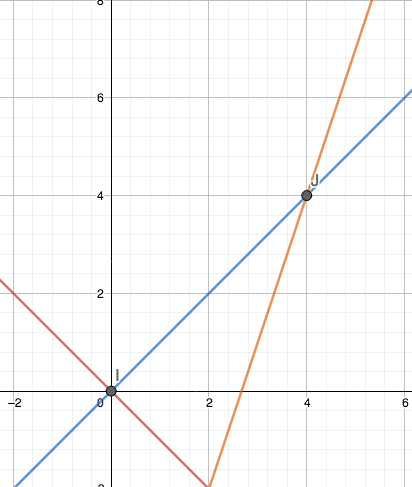
To find three expressions where the first one is the biggest when $n\lt0$, the second one is the biggest when $0\lt n\lt4$ and the third is the biggest when $n\gt4$ the intersections of the first and second line need to be $x=0$ (Point I) and the intersection of the second and third line needs to be $x=4$ (Point J).
With the graph it is visually demonstrated which value is the largest at any value of $n.$
The equation of the first expression (red) is $-n$
The second expression (blue) is $n$
The third expression (orange) is $3n-8$
Adithya used a quadratic expression:
The first expression which must be biggest whenever $n\lt0$ is $-n$ and the third expresion which is the biggest whenever $n\gt4$ is $n-4.$
Justin constructed the expressions algebraically:
Let's start with the expression $n+10$. If this expression is bigger than the second expression whenever $n\lt0,$ then the first and second expressions must be equal when $n=0.$ Let's set the coefficient of the second expression to $2,$ and label the constant $c.$ Then:
$(0)+10=2(0)+c$
$\Rightarrow 10=c$
The second expression is $2n+10.$ We know that $2n+10$ is greater when $n\gt 0$ and $n+10$ is greater when $n\lt0$ and not vice versa through trial and error:
$(1)+10 \lt 2(1)+10$
$\Rightarrow 11<12$
If $2n+10$ is bigger than the third expression whenever $0\lt n \lt 4$, then the second and third expressions must be equal when $n=4.$ Let's set the coefficient of the third expression to $3,$ and label the constant $c.$
$2(4)+10=3(4)+c$
$\Rightarrow 18=12+c$
$\Rightarrow 6=c$
The last expression is $3n+6.$ We know that $3n+6$ is greater when $n\gt4$ and $2n+10$ is greater when $n\lt4$ and not vice versa through trial and error:
$2(5)+10\lt3(5)+6$
\Rightarrow $20\lt 21$
$5\gt4$, $2n+10\lt3n+6$.
$2(3)+10\gt 3(3)+6$
$\Rightarrow 16\gt15$
$3\lt4$, $2n+10\gt3n+6$.
Assuming $n+10$ is the first expression, the three expressions are $n+10$, $2n+10$ and $3n+6$.
Find three expressions so that the first is biggest whenever $n\lt3$, the second is biggest when $n\gt3,$ and the third is never the biggest.
Clara: $-n+5$, $n$ and $n-100$
Adithya and Justin used graphical solutions. Adithya used parallel lines:
The three expressions would be $-n-3,$ $n+3$ and $n.$
Graphically this produces the following (the blue line represents $-n-3,$ the purple line represents $n+3$ and the black line represents $n$
Justin used a quadratic:
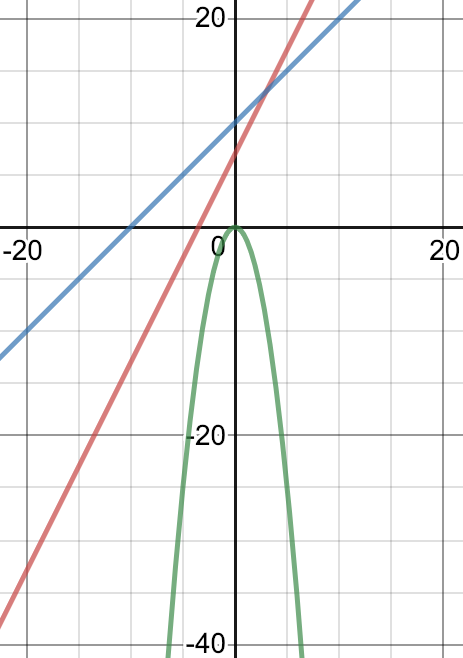 A quadratic graph with a negative coefficient would satisfy the requirement of never being the biggest, as both ends would curve downward. If the quadratic graph is the biggest at one point, we could decrease the constant or move it left/right across the x-axis. In
this case, none of this necessary. The graph of $-n^2$ is in green:
A quadratic graph with a negative coefficient would satisfy the requirement of never being the biggest, as both ends would curve downward. If the quadratic graph is the biggest at one point, we could decrease the constant or move it left/right across the x-axis. In
this case, none of this necessary. The graph of $-n^2$ is in green:Find three expressions so that one of them is the biggest regardless of the value of $n.$
Find three expressions so that one of them is the biggest regardless of the value of $n.$
Again, Clara found three which work for whole numbers:
$n^2+5$, $n+4$ and $n+5$
$n^2$ was really useful because it meant that if $n$ was negative $n^2$ would make it positive.
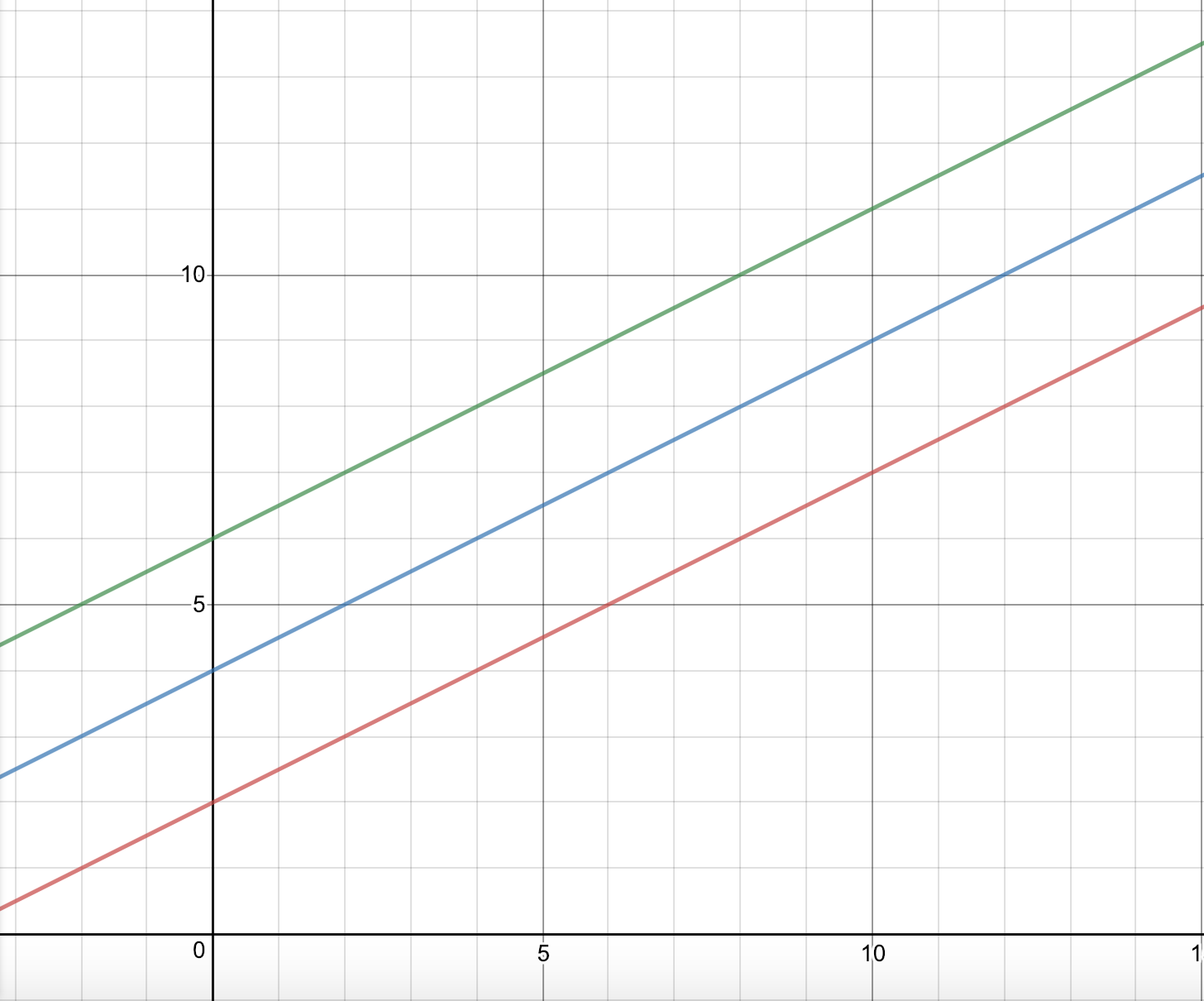
Adithya, Ana and Justin all used parallel lines. This is Justin's work:
If three lines in a plane are parallel, they will not intersect - the biggest will not change. Lines that are parallel have the same slope. Then, the expression with the highest constant will be biggest.
Since the specific numbers do not matter as long as the coefficients are the same, we can just choose any numbers - let's say $\frac{1}{2}n+2$, $\frac{1}{2}n+4$, and $\frac{1}{2}n+6.$
The graph below shows that $\frac{1}{2}n+6$ is biggest regardless of the value of $n$:
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Doesn't Add Up
In this problem we are faced with an apparently easy area problem, but it has gone horribly wrong! What happened?
From All Corners
Straight lines are drawn from each corner of a square to the mid points of the opposite sides. Express the area of the octagon that is formed at the centre as a fraction of the area of the square.