Copyright © University of Cambridge. All rights reserved.
'Shaping It' printed from https://nrich.maths.org/
Show menu
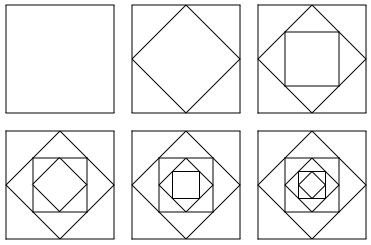
You can, of course, start with any straight-lined shape.
Here's one where I've coloured each new halving line to help to see what has happened more clearly.
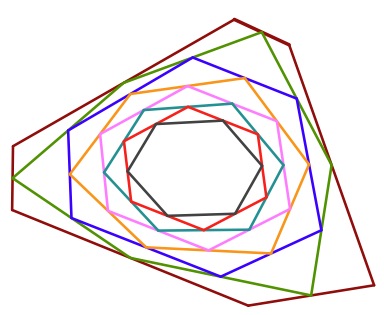
So, it's your turn to have a go.
It's probably good to start with a fairly large shape since it's going to get smaller and smaller each time.
Here are some challenges for you to
pursue:
- Having made a design like one above, cut out the triangles and the smallest inner shape and rearrange the pieces to form a new shape/design.
- Talk about and record the things you notice as you have drawn more and more halving lines.
- What is happening to the enclosed area each time the sides are halved? (Try investigating a regular shape first.)
This problem is based on an idea
suggested by Ian Short.