 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
ABC



- Problem
- Student Solutions
In the multiplication below, some of the digits have been replaced by letters and others by asterisks. Where a digit has been replaced by a letter, the same letter is used each time, and different letters have replaced different digits. Can you reconstruct the original multiplication?
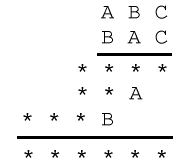
The following splendid solution, from Prav at the North London Collegiate School Puzzle Club, gives a clear and full explanation of all the reasoning required to solve this problem. Very well done Prav!
The answer is as follows:

I will now try to explain how I found my answer. We know that when ABC is multiplied by A the answer is a three-digit number. This means that A is an integer of value less than or equal to three. We also know that when A is multiplied by C the resulting answer is a number which ends in A, i.e. A * C = XA.
This means that A cannot be 1 because the only digit multiplied by 1 to end in a number whose last digit is 1 is 1 itself and A and C cannot be the same number. Also the value of C cannot be 1 because ABC multiplied by C would then be a 3 digit number instead of a 4 digit number.
We know A cannot be three because there is no digit C, which multiplied by 3, will equal X3.
Therefore our only possibility is that A is equal to two.
Because A * C = XA we can substitute A=2 into the formula. so 2 * C = X2.
The only digit which multiplied by 2 has 2 as the units digit 6, this is because 2 * 6 = 12.
We also know that B * C = XB. We now know that C = 6 so we can substitute this into the formula too.
B * C = XB
B * 6 = XB
The possibilities for B are 4, 6 and 8.
We know that B can not be 6 because C is 6 and both numbers can not be the same. Also B can not be 4 because when ABC is multiplied by B the answer is a 4-digit number but if B were 4 then we would have 246 * 4. This results in 904, which is not a 4-digit number, so the only possible remaining digit is 8. When substituted in the formula it works, as shown above.
So our final answer is that A = 2, B = 8 and C = 6!!!