At Least One... printable sheet

Imagine flipping a coin three times.
What's the probability you will get a head on at least one of the flips?
 
Charlie drew a tree diagram to help him to work it out:
 
 
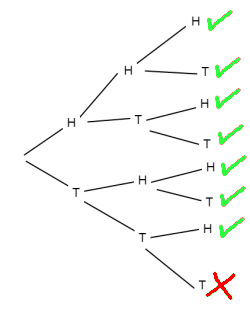
He put a tick by all the outcomes that included at least one head.
How could Charlie use his tree diagram to work out the probability of getting at least one head?
How could he use it to work out the probability of getting no heads?
What do you notice about these two probabilities?
 
Devise a quick way of working out the probability of getting at least one head when you flip a coin 4, 5, 6... times.
What is the probability of getting at least one head when you flip a coin ten times?

Once you've worked out a neat strategy for the coins problem, take a look at these related questions which can be solved in a similar way:

Imagine choosing a ball from this bag (which contains six red balls and four blue balls) and then replacing it.

If you did this three times, what's the probability that you would pick at least one green ball?

What if you didn't replace the ball each time?
 


Imagine a class with 15 girls and 13 boys.
Three children are chosen at random to represent the class at School Council
What is the probability that there will be at least one boy?

 

Why not try the problem Same Number! next?