Copyright © University of Cambridge. All rights reserved.
'Journeys in Numberland' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem will give learners a chance to make predictions and generalisations. It also provides practice in simple addition and subtraction, and later in multiplication and division. It draws out the inverse relationship between the pairs of operations but it also encourages children to think about the order of operations.
You will need copies of this sheet, and for the second part of the problem this sheet. Squared paper might also be useful.
Possible approach
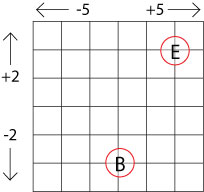
You could start by showing the first part of the problem to the whole group and by explaining the setting for the problem. A small scale version could be drawn out on the playground or on the hall floor so that the game can be played practically. The first 'journeys' of both boys could be worked out at this stage.
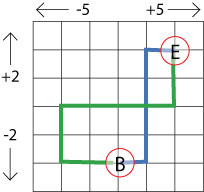
After this introduction, the group could work in pairs so that they are they are able to talk through their ideas with a partner, using copies of the first sheet. Encourage them to find interesting routes that use subtraction as well as addition. Routes can be drawn using different colours but pairs may well need more than one copy of the sheet. Children may need to use jottings
to keep track of their calculations and these could be done on paper or mini whiteboards, for example.
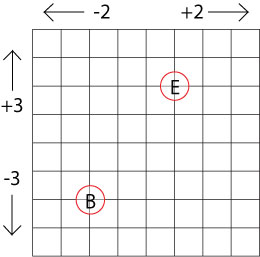
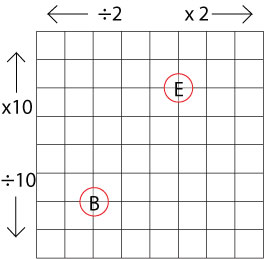
Before having a go at the second part of the problem (multiplication and division), encourage pairs to predict what they think might happen. You may feel that calculators could be used for checking results at this stage.
At the end of the lesson, bring the whole group together again to discuss their findings. They could show their most interesting and/or longest routes. Were they surprised by the results? Why do they think this happened? Although this task focuses only on numerical operations, the explanation of the results demands a very sound understanding of the number system.
Key questions
Can you find a more interesting way to go that uses subtraction as well as addition?
Do you notice anything about those answers?
Can you find a more interesting way to go that uses division as well as multiplication?
Would it be a good idea to use a calculator to check those results?
Can you explain your findings?