Perimeter expressions
Create some shapes by combining two or more rectangles. What can you say about the areas and perimeters of the shapes you can make?
Problem
Perimeter Expressions printable worksheet

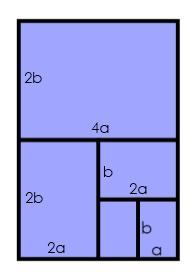
Charlie took a sheet of paper and cut it in half.
Then he cut one of those pieces in half, and repeated until he had five pieces altogether.
He labelled the sides of the smallest rectangle, $a$ for the shorter side and $b$ for the longer side.
Here is a shape that Charlie made by combining the largest and smallest rectangles:
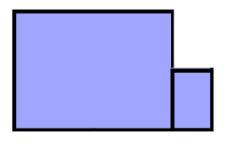
Check you agree that the perimeter is $10a + 4b$.
Alison combined the largest and smallest rectangles in a different way. Her shape had perimeter $8a + 6b$. Can you find how she might have done it?
Charlie and Alison made sure their rectangles always met along an edge, with corners touching.
Can you combine the largest and smallest rectangles in this way to create other perimeters?
Create some other shapes by combining two or more rectangles, making sure they meet edge to edge and corner to corner. What can you say about the areas and perimeters of the shapes you can make?
If you have a friend to work with, you could each create a shape and work out the area and perimeter. Can you recreate each other's arrangement if you only know the area and perimeter?
Here are some questions to consider:
What's the largest perimeter you can make using all the pieces?
Can you make two different shapes which have the same area and perimeter as each other?
Can you make two different shapes which have the same perimeter but different areas?
How do you combine any set of rectangles to create the largest possible perimeter?
Charlie thinks he has found a shape with the perimeter $7a + 4b$. Can you find his shape?
What can you say about the perimeters it is possible to make, if $a$ and $b$ are the dimensions of one of the other rectangles?
This problem is based on an idea shared by Sue Southward.
Getting Started
Here are the dimensions of all the rectangles:
Student Solutions
Daniel from Staplehurst Primary School sent us a very clear solution to this problem:
Alison's shape with a perimeter of 8a + 6b combined the largest and smallest rectangles, with the smaller rectangle's side of length a against one of the larger rectangle's sides.
I have made the largest possible perimeter, 12a + 12b, using all the pieces because I have put the shorter side of each shape against the one before it.
Click here to see the examples and all the working out.
Rajeev from Haberdashers' Aske's Boys' School managed to improve on Daniel's solution for the largest perimeter. Take a look here at how he combined the rectangles.
Daniel also considered one of the later questions:
I would like to see Charlie's second shape with a perimeter of 7a + 4b because I think he has made a mistake: it is impossible to find a shape with an odd number of "a"s.
It is impossible to get an odd number of "a" or "b" on the perimeter because every shape has an even number of "a"s or "b"s. When you place the a against an existing shape you are taking away an a from the perimeter and then adding one back again as well as adding 2b and vice versa, this is true with all the rectangles that you add on. Therefore you always get an even number of "a" or "b".
Benjamin from Wilson's School agreed:
I noticed that whatever way you arrange the two rectangles, the perimeter always equals:
(the longest length + the longest width) x 2
Teachers' Resources
Why do this problem?
This problem gives students plenty of opportunity to practise manipulating algebraic expressions within a purposeful context. Along the way, the challenges will provoke some insights that will be worth sharing. Issues relating to the dimensions in formulae for areas and lengths might emerge.
Possible approach
This printable worksheet may be useful: Perimeter Expressions.pdf
The worksheet is also available in French: Expressions de périmètres
We are grateful to Clara Huizink for translating the original.
Hand out sheets of paper (A4 is ideal) and introduce the problem, giving students time to cut out their five rectangles.
Show the image of Charlie's shape and ask students to work out the perimeter in terms of $a$ and $b$. The area of the smallest rectangle could be designated $R$ and used as a unit to express other areas, if students are not confident enough in their algebra to express it in terms of $a$ and $b$.
Once everyone is happy that the area is $9R$ or $9ab$ and the perimeter is $10a + 4b$, ask them to combine the largest and smallest rectangles (edge to edge, corner to corner) to make other shapes, and work out the areas and perimeters. How many different perimeters can they find?
Once they have done this, discuss: are they surprised that they only found one other possible perimeter, and that the two answers could be reached in several different ways?
The next challenge is to make different shapes using at least two of the rectangles, and again work out the area and perimeter. Students could make a shape in pairs and work out the area and perimeter to give to another pair (without letting them see the shape), to see if they can create a shape with the same area and perimeter. There is opportunity for fruitful discussion when the two shapes are compared, to see what is the same and what is different, and to see if one can be transformed into the other.
Alternatively, collect together the areas and perimeters on the board. Then in pairs, challenge students to combine rectangles to make each of the area/perimeter combinations listed on the board, checking each other's work as they go along.
Finally, the "questions to consider" provide some interesting points for discussion - students could be invited to suggest questions they think mathematicians might ask themselves, with the list in the problem used to prompt ideas if necessary.
Key questions
How do we know whether an expression represents an area rather than a perimeter?
Possible extension
Number Pyramids builds on this activity by challenging students to create algebraic expressions to explain a relationship.
Possible support
Use numerical values, instead of $a$ and $b$, and cut the rectangles out from squared paper. Begin by looking for numerical relationships rather than algebraic ones, and perhaps introduce the algebra to explain the patterns students find.
