The Add and Take-away Path printable sheet

Once there was a garden with lots of paths and little patches of grass between them. It looked a bit like this:

Two children, William and Thea, made up a game.

For every patch of grass they passed as they walked to the right on the picture, they added one.
For every patch of grass they passed as they walked to the left on the picture, they took away one.
If they went North (up on the picture), they added two for every patch of grass, and if they went South (down on the picture), they took away two for each patch of grass.

They started with ten points at S, and added and took away until they reached E.

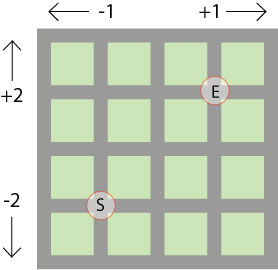
These are the paths they took:

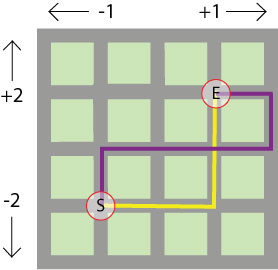
Thea took the yellow path. Remember she started with $10$ points.
How many points did she have when she arrived at E?

William took the purple path.
How many points did he have when he arrived at E?

In the picture below, we've taken out the grass and just drawn a grid. You can imagine that the squares are patches of grass and the lines are the paths in the garden.
 
We have marked different starting and end points.
What would your score be if you walked along the blue path?  
And the red path?

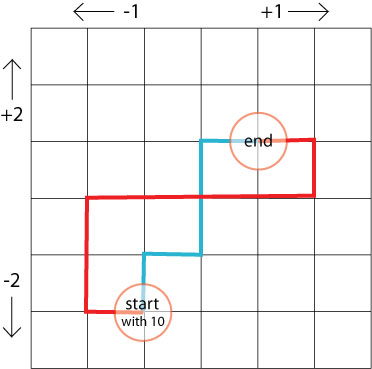
Make up some more paths between these start and end points.
What is your score each time?
What do you notice?
Can you explain why?