Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Area and Perimeter
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Area and Perimeter
What can you say about these two shapes?

What is the area of each one? What is the perimeter of each one?
What can you say about the shapes below?
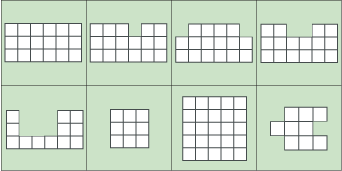
You can print out a set of shapes and cut them into separate cards. These cards have the coloured background.
Can you draw a shape in which the area is numerically equal to its perimeter? And another?
Can you draw a shape in which the perimeter is numerically twice the area?
Can you draw a shape in which the area is numerically twice the perimeter?
Can you make the area of your shape go up but the perimeter go down?
Can you make the perimeter of your shape go up but the area go down?
Can you draw some shapes that have the same area but different perimeters?
Can you draw some shapes that have the same perimeter but different areas?
Why do this problem?
This problem offers opportunities for children to consolidate their understanding of area and perimeter. The exploratory nature of the task means that learners will be grappling with the two concepts at the same time rather than tackling them independently which might usually be the case. The activity is likely to require persistence and a 'tinkering' or trial and improvement approach.
Possible approach
It is essential to have squared paper available (preferably $1$ cm squared) and the shapes printed out and cut into eight separate cards. These cards can be downloaded here in black and white, and here with a coloured background. It might also be helpful to have post-it notes so that pupils could attach details of area and perimeter onto each card, rather than continually having to re-calculate them.
You could start with the whole group looking at the two shapes given at the beginning of the problem and invite learners to talk about anything they notice. (These are also two of the shapes given on the set of cards.) If area and/or perimeter doesn't come up naturally, you could ask direct questions to shift their attention to these concepts.
Pairs could then explore the shapes on the remaining cards and you can challenge them with the specific questions given in the problem itself. Copies of the task and questions for printing out can be downloaded here. It is important that you stress we are looking at numerically equal values. The area and
perimeter cannot be equal because they are measured in different units.
When you gather the whole group together again, invite them to share not just solutions (i.e. shapes that fit the criteria), but their methods for creating the shapes. Did they establish any 'principles' that helped them? What actions could they perform on a shape without changing its perimeter? For example, what happens to the area and perimeter if you take a 'corner
square' off a shape? What happens if you take an 'edge square' off a shape? What happens if you take a 'middle square' out of a shape? It may be that some children notice that for a given perimeter, a square gives the maximum possible area.
Key questions
How will you find out the perimeter?
How will you find out the area?
Tell me about that shape.
It might help to use squared paper to try out your idea.
How could you make the area of that shape bigger/smaller? How will that affect its perimeter?
How could you make the perimeter of that shape bigger/smaller? How will that affect its area?