Copyright © University of Cambridge. All rights reserved.
'Walkabout' printed from https://nrich.maths.org/
Show menu
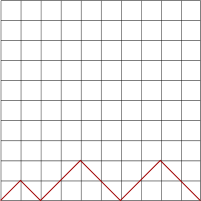

A walk is made up of diagonal steps, starting at the bottom left and ending up back on the bottom line (x-axis). You can move diagonally up and down towards the right but you cannot move towards the left.
A diagonal must go from a left-hand corner of a square to the opposite right-hand corner of the same square.
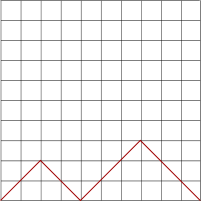
The examples above all show 10-step walks. So let's look at a 2-step walk in more detail:
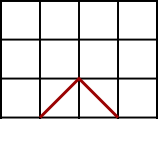
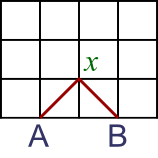
There is only one way to make a 2-step walk - from A up to x and down to B:
Here are two 4-step walks:
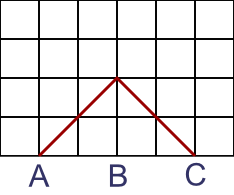
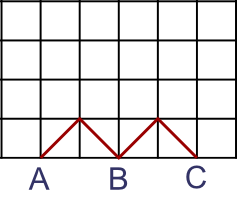
Are there any more 4-step walks?
How do you know you have them all?
How many 6-step, 8-step walks are there?
Can you find a general rule?
See also the problems One Basket and Counting Binary Ops