Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Three Sets of Cubes, Two Surfaces
Age 7 to 11
Challenge Level 





- Problem
- Teachers' Resources
Three Sets of Cubes, Two Surfaces
This can be used as a follow-on from Two on Five.
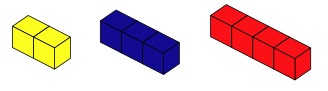
You have interlocking cubes of three different colours - 2 of one colour, 3 of another colour and 4 of the third colour.
It could look like this;
This is slightly different from Two on Five but is seen as an extension for some pupils. You might like to go there first!
The nine cubes are to be connected in the usual way with the following rules being applied.
The two yellow cubes are not allowed to touch the wall or floor surfaces
The Three blue cubes must touch one surface only, the wall or the floor
The four red cubes must touch both wall and floor surfaces
Here are two examples that obey the rules;
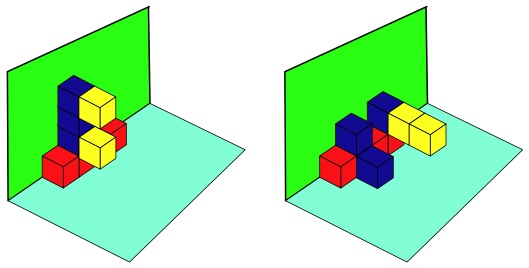
See what others you can find.
How many will there be?
At some point ask yourself "I wonder what would happen if I ...?"
Possible approach
As this is designed for the highest attaining, it might be presented as on the website or in a one-to-one situation, encouraging discussion between adult and pupil. The pupils may need access to a computer program for drawing solutions.
Key questions
Tell me about what you have found.
Can you describe the ways that you arrived at these shape arrangements?
How did you construct these on the computer?

