Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Sitting Round the Party Tables
Age 5 to 11
Challenge Level 





Sitting Round the Party Tables printable sheet
Some children are at a party. They are sitting around a square table like this:
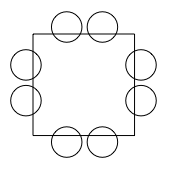
In the top left-hand corner is the person who is giving the party. They have a bag of sweets and they start giving them out in a clockwise direction: one for themselves, two for the next person, three for the next and so on.
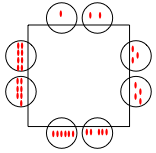
What do you notice?
You might like to focus on:
- The number of sweets that are given out altogether
- The total number of sweets that children sitting opposite each other are given
- The total number of sweets that children sitting diagonally opposite each other are given
- Or something else!
There are other similar parties happening at the same time. They have bigger square tables with more children sitting around them - perhaps 3 children on each side, or maybe more.
Draw some of these tables. What do you notice? You can choose one of the areas above to focus on, or you might have your own ideas about what to investigate.
Once you've thought about that, you might like to explore what happens with five- and six-sided tables like these:
What do you notice?