This challenge led to some interesting submissions. Some were extra thoughtful and tried to explain why some of these problems were impossible to solve.

Srimoyi from Bushey Heath Primary sent in the following:

Problem 1: 123

Problem 2: No solution

Possible number combinations in arranging 1 2 3 & 4 is as below. First digit and third digit can be 1 or 3. Second and Fourth digit can be 2 or 4.
3 2 1 4 --> Not divisible 4 when considering all 4 digits
3 4 1 2 --> Not divisible by 3 when considering 3 digits
1 2 3 4 --> Not divisible by 4 when considering all 4 digits
1 4 3 2 --> Not divisble by 3 when considering 3 digits
Hence no solution possible

Problem 3: 34125

Possible number combinations in arranging 1 2 3 4 5 is as below. First digit and third digit can be 1 or 3. Second and Fourth digit can be 2 or 4. Fifth digit has to be 5 only.

12345  --> Not divisble by 4 when considering 4 digits only
14325  --> Not divisble by 4 when considering 4 digits only
32145  --> Not divisble by 4 when considering 4 digits only
34125  --> Answer, works for all criteria

Thank you for sharing your thinking with us, Srimoyi - there are lots of good ideas here. Isobel, Charlotte and Bella from St. Andrew's School, North Weald pointed out that there is one "slip up" in this solution. Thank you so much for being keen eyed to see the "slip up". Maybe others can find the "slip up" too.

Salvia from Westridge School in America explained her thinking:



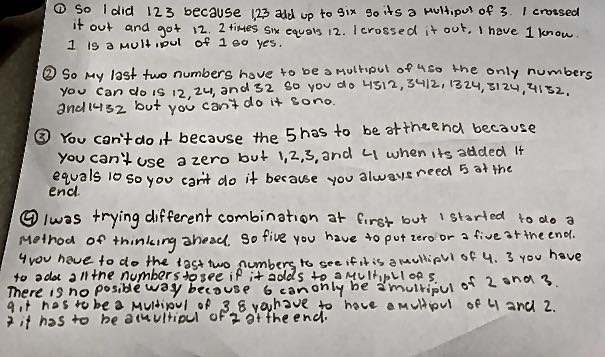
Here we have a number of solutions from Peak School in Hong Kong.

Victoria
1. 1,2,3 or 3,2,1
2. impossible: some 4 digit numbers are divisible by 4, but not divisible by 3 example: 4321/4=1078 and 4321/3=1440r1
3. impossible:because it must be a 5 at the unit place,but the 4 times table does not have any numbers end in 5  example: 4x1=4. 4x2=8. 4x3=12. 4x4=16

Marcus and Quinton
3 divided by 321 = 107 and 3 divided by 123 = 41
What systems are you using? Long division and bus stop method

Mathias & Haider
We did the first one and it went well. Then for the second one there was no possible answer because for the first answer for the 1,2,3,4 there was a remainder. For the curious number we used the bus stop method because it comes very handy when you do division. A pattern was that there should have been 2 even answers for each set of numbers.

Nicholas and Sophie
First we quickly found out that there were 2 answers for the first question.
The first one was the number 321 and the other number was 123.
The second question was a bit tricky because now there were 4 digits instead of 3 digits. We started to guess and check. We figured that this would be the easiest way to solve the problem. An easy way to recognise multiples of 3 is if the digit sum is a multiple of 3. A way to recognise multiples of 4 is if the end digit/s are multiples of 4. The quickest way to find multiples of 5 is if the number ends in 5 or 0.

Jaiman & Pradeep
1: 123, 321
2: NO POSSIBLE ANSWER
3: NO POSSIBLE ANSWER
WE USED: Guess Check and Improve
÷3 Sum is a multiple of 3
÷4 Last two numbers are divisible by 4
÷5 End in 5 or 0
÷6 Is a multiple of 2 and 3
÷8 Last two numbers are divisible by 8
Rule: Any number is over 1,2,3,4 will work or have an answer

Audrey, Hayley, Holly, Anna
We think that we have found two solutions for the first question:
123 / 3 = 41  12 / 2 = 6   1 / 1 = 1    or   321 / 3 = 107   32 / 2 = 16  3 / 1 = 3

We think that there is no solution for the question for 1, 2, 3, 4. We kept trying different number orders and tried to divide them by 4, and some of them worked, but when we moved on, the division equation didn't work. A rule that we found was the number that we were dividing had to have a pattern that goes odd, even, odd, even.  The reason we think this is because it has to be divided by 4, then divided by 2. Odd, even (divide by 2), odd, even (divide by 4).

We don't think that there will be any other numbers that work above 4 because since we can't find any solutions for 4, then it will always come back to 4 so it will never work.

Dorika, Tanya, Isabella and Ian
For the first question we found 123 and 321. 123 because 123÷3=41, 12÷2=6 and 1÷1=1. 321 because 321÷3=107, 32÷2=16 and 3÷1=3.

For the 2nd and 3rd question we could not find an answer because the digits could not fit in an order while still completing the criteria and so that all numbers are whole numbers.
The systems we were using are long division, mental division and guess and check. What we found out about numbers 3, 4 and 5 were that to be divisible by 3 the digit sum has to be a multiple of three, to be divisible by 4 the last 2 numbers have to be a multiple of 4 and to be divisible by 5 the last digit has to be 5 or 0.

Zach and Coen
The answer for the first question is 123 and 321 because when you add up the digit sum, it equals 6 and 6 is a multiple of 3.
The second question is not possible.
The answer for the third question is all the numbers that end in 5 because multiples of 5 end in 5 or 0.
The systems that we were using is guess and check, long division and mental strategies. What we know about numbers that can be divided by 3, 4, or 5 is that 5 has to end in 5 or 0, the digit sum equals 6 which is a multiple of 3 and 4 doesn't work.

Finally Chloe & Victoria
1. 1) 123 and 321
2. How? 1)  123: 3 =  41; 12: 2 = 6; 1: 1 = 1  2)  321: 3 = 107; 32: 2 = 16; 3: 1 = 3
1. 2) No answer
1234: 4 = 308 r2 X;   1243: 4 = 310 r3 X;   1423: 4 = 355 r3 X;   1432: 4 = 358;    143: 3 = 35 r3 X;   2431: 4 = 607 r3 X;  
2413: 4 = 603 r1 X;   3214: 4 = 803 r2 X;   3241: 4 = 810 r1 X;   3421: 4 = 855 r1 X;   3412:4 = 853;   341:3 = 112 r3 X;   4213: 4 = 1053 r1 X;   4231: 4 = 1057 r3 X 

Thank you all for sending in these ideas! Some children thought that because it was impossible with 1, 2, 3 and 4, it would be impossible with 1, 2, 3, 4, 5, 6, but actually because you can use the 6 to help you in the first part of the number, there are some possible solutions. Hwan from Hong Kong International School described the solutions for each version of this challenge:

Number 1: 123.
123 divided by 3= 41
12 divided by 2= 6
1 divided by 1= 1
Number 2: No solution
Number 3: No solution
Challenge Problem: 123654 or 321654

Thiyara from The Woodside Academy also found the same two solutions with 6 digits:

The answer for 6 digits is 321654 or 123654 because it is divisible by every number up to 6 when you take away a number starting from the right. To work out my answer, I knew that the 5 had to go in the tens because the rule of divisibility for 5 is that the number ends in 0 or 5 and 0 was not an option. I knew that the digits in the units, hundreds and ten thousands had to be even and the others had to be odd. So from there I used trial and error until I got an answer that worked.

Well explained, Thiyara! I wonder if there's a quicker way to work this out than trial and error?