Copyright © University of Cambridge. All rights reserved.
'Your Number Was...' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem provides a great opportunity to introduce the concept of representing operations on unknown numbers algebraically. It leads to work on inverse operations and solving simple linear equations. When first shown the interactivity, students may be amazed and astonished that it can always work out the starting number. The intention is to provoke their curiosity so they become
determined to explain the mystery.
Possible approach
You may wish to work on the problem Your Number Is... before trying this.
Either work through a few examples using the interactivity, or read out the instructions:
Think of a number
Add 4
Double
Subtract 7
Ask a few students what they finished with and then surprise them by revealing their starting number!
As we don't want students to end up thinking maths is a strange magical mystery, it's time to explain what's going on!
One way to begin thinking about this is to collect together some outputs and their corresponding inputs, for example:
One way to begin thinking about this is to collect together some outputs and their corresponding inputs, for example:
| Finishing Number | Starting Number |
| 11 | 5 |
| 17 | 8 |
| 3 | 1 |
| 23 | 11 |
| 14 | 6.5 |
This is not merely an exercise in pattern spotting - once learners have figured out HOW the machine is working out the starting numbers, they need to understand WHY this works.
It would be good to introduce a variety of methods for explaining what's going on:
- Represent the instructions as a function machine, and explore what happens when the functions are inverted.
- Represent the chosen number as $x$ and write an expression for the final number $y$ in terms of $x$. Then rearrange to get $x$ in terms of $y$.
- Discuss simplification to make the functions easier to invert (so representing it as $y=2x+1$ rather than $y=2(x+4)-7$.
Now challenge the class to come up with their own examples of "Think of a number" instructions, which they can invert to deduce someone's starting number from their final number. Encourage them to record their working using function machines and algebra. Set challenges such as having to include particular operations, at least 6 different operations, and a set of instructions that's really
quick to invert.
At the end of the lesson, a selection of students can read out their instructions for the class to try, and then work out starting numbers from the final numbers.
In the "Settings" menu for the interactivity, you can edit the functions used by the machine. Click below to learn more.
At the end of the lesson, a selection of students can read out their instructions for the class to try, and then work out starting numbers from the final numbers.
In the "Settings" menu for the interactivity, you can edit the functions used by the machine. Click below to learn more.
To access the settings menu, click on the purple cog in the top right corner of the interactivity. The screenshot below shows the menu:
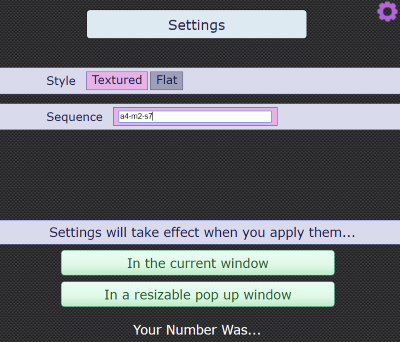
You can enter your own sequence, separated by hyphens, using the code "a" for add, "s" for subtract, "m" for multiply and "d" for divide. The sequence a4-m2-s7 in the screenshot represents "Add 4, Multiply by 2, Subtract 7".
Once you have entered your chosen sequence, click to load it in the current window or a new resizable window.

You can enter your own sequence, separated by hyphens, using the code "a" for add, "s" for subtract, "m" for multiply and "d" for divide. The sequence a4-m2-s7 in the screenshot represents "Add 4, Multiply by 2, Subtract 7".
Once you have entered your chosen sequence, click to load it in the current window or a new resizable window.
Key questions
How does the computer "know" what your starting number was?
If you think of a number and add four, what do you need to do to get back to where you started?
If you think of a number, add four, and then double, what do you need to do to get back to where you started?
Is there a way of representing the "Think of a number" trick that helps you to get back to the starting number?
If you think of a number and add four, what do you need to do to get back to where you started?
If you think of a number, add four, and then double, what do you need to do to get back to where you started?
Is there a way of representing the "Think of a number" trick that helps you to get back to the starting number?
Possible support
In the problem Your Number Is..., students can explore visual and symbolic ways of representing number tricks.Possible extension
Think of Two Numbers is a challenging extension.